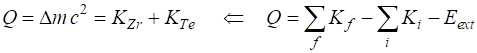|
SPECIAL RELATIVITY and NUCLEAR REACTIONS NUCLEAR FISSION |
|
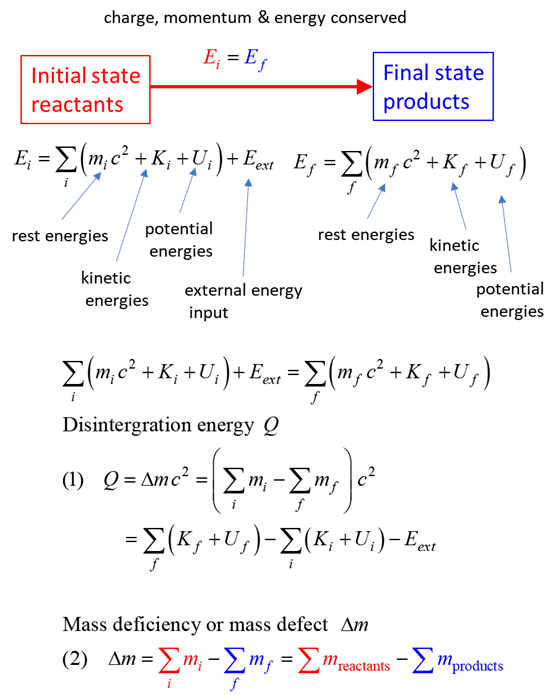
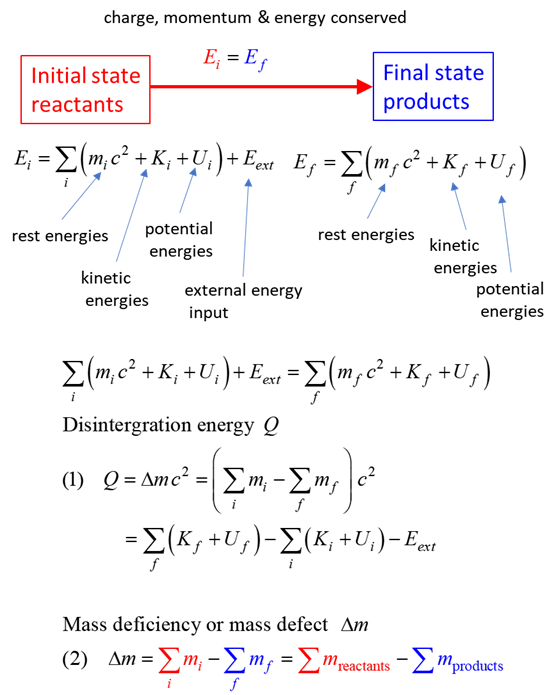
SUMMARY Total energy total
energy = rest energy + kinetic energy + potential energy
Law of
conservation mass-energy isolated
system E =
constant
NUCLEAR FISSION A very significant nuclear
transmutation which is initiated by a neutron is called nuclear fission. In this
transmutation, which can only take place when certain heavy nuclei such as 235U92
absorb an incoming neutron. The heavy nucleus then splits into two lighter
nuclei (fission fragments) with two or more other neutrons being released.
The mass of products is less than original mass of the nucleus that splits.
The energy liberated is mainly the kinetic energy of the products. |
|
Energy / Mass units, values and conversion factors amu (atomic mass unit) = 1 u = 1.66054´10-27 kg 1 eV = 1.602´10-19 J 1 MeV = 106 eV A mass of 1 u
(1 amu) has an energy equivalent of: E = (1.66054´10-27) (2.99792´108)2 J = 1.49242´10-10 J E = 931.494
MeV 1 u º 931.494 MeV/c2 Proton mass mp = 1.67262´10-27 kg = 1.0072765 u = 938.3 MeV/c2
Neutron mass mn = 1.67493´10-27 kg = 1.0086649 u = 939.6 MeV/c2 Electron mass me = 9.1093897´10-31 kg = 0.0005485799 u = 0.511
MeV/c2 NUCLEAR REACTIONS
NUCLEAR FISSION A very significant nuclear
transmutation which is initiated by a neutron is called nuclear fission. In this transmutation, which can take
place when only certain heavy nuclei such as 235U92
absorb an incoming neutron. The heavy nucleus then splits into two lighter
nuclei (fission fragments) with two or more other neutrons being released. The
mass of products is less than original mass of the nucleus that splits. The
energy liberated is mainly the kinetic energy of the products. This is how
energy is released in nuclear power reactors and in atomic bombs.
Usually the fragments are unstable,
and a series of radioactive decays occur until stable nuclei are formed. This
is why the fallout
from a nuclear reactor accident or an atomic bomb blasts are highly
radioactive and potentially fatal to many life forms. Typical fission reactions are: 235U92
+ 1n0 à 236U92* à 144Ba56 + 89Kr36
+ 31n0 235U92
+ 1n0 à 236U92* à 140Xe54 + 89Sr38
+ 21n0 The contributions to the energy
released in a typical fission of a heavy nucleus are: ·
~ 84% appears as kinetic energy of the
fission fragments. ·
~ 3% appears as kinetic energy of the
released neutrons. ·
~ 3% emission of gamma
rays. ·
~ 10% given off in the radioactive
decay of the fission fragments. |
|
Example 1 Calculate the Q
-value of the induced fission reaction
initial state (reactants)
uranium-235
235U92 + 1n0 mU235
= 234.993462 u mZr = 98.894721 u mTe = 133.882843 u mn = 1.008665 u
(nuclear mass used)
Mass deficiency Note: mass of uranium nuclei is
greater the sum of the masses of the zirconium and tellurium. Disintegration energy Mass: Reactants 234.993462 u
1.008665 u
Mass: Products 98.894721 u
133.882843 u
3.025995 u
Mass defect dM = 0.198568 u
Disintegration value Q Q = 184.965194
MeV The energy released in the fission
reaction appears mainly as the kinetic energy of the zirconium and tellurium
nuclei. Since Q
>
0, this reaction can occur spontaneously. This is a tremendous amount of energy released in a
single fission of one uranium nuclei. At a macroscopic level, this energy
released is tiny. However, many such fissions would occur in a short time and
at a macroscopic level the energy released is enormous. 235U92
EB = 1784 MeV
EB / nucleon = 7.6 MeV
99Zr40
EB = 845 MeV
EB
/ nucleon = 8.5 MeV 134Te52
EB = 1123 MeV
EB / nucleon = 8.4 MeV The binding energy of uranium-235 is
7.6 MeV per nucleon, but the fission fragments of intermediate mass of
binding energy per nucleon on average of about 8.4 MeV. Since, the fission
products are more tightly bound, they have less mass. The difference in
binding energy between the uranium nuclei and the fragments is about 0.8 MeV
per nucleon. Since there are 235 nucleons involved in each fission, the total
energy release is about 190 MeV (0.8x235 = 190). This mass difference
accounts for the tremendous energy released in a single fission event. What is the energy released by the fission of 1.00 kg of 235U92? 1 mole of uranium 235
number of atoms
(Avogadro’s number) NA
= 6.022140857x1023
molar mass M
= 235.043931368 x10-3 kg (neutral atom) mass of single uranium 235 atom m = M
/ NA mass of sample of uranium 235 mU
= 1.00 kg number of atoms in sample N = mU / m
m = mU
/ N Hence, N = mU NA / M Total energy released by fission of
1.00 kg uranium 235 mU
= 1.00 kg
NA = 6.022140857x1023 M
= 235.043931368 x10-3 kg
N
= 2.6x1024
atoms Q
= 185 MeV = (185)(1.602x10-13) J = 2.96x10-11 J QU ~
7.6x1013 J This is an enormous amount of energy !!!
|
|
Example 2 Calculate the energy released in the
nuclear fusion reaction 235U92
+ 1n0 à 236U92*
à 136Xe56
+ 88Sr36 + 121n0 Conservation of energy –
assume initial and final kinetic energies neutrons are negligible Mass: Reactants 234.993462 u
1.008665 u
Mass: Products 87.884766 u
135.877591 u
12.103979 u
Mass defect dM = 0.135790 u
Disintegration value Q Q = 126.487864
MeV Compare with Example 1. The fission fragments are different. |
|
Example 3 What initial mass of 235U92
is required to operate a 500 MW reactor for 1 year? Assume 40% efficiency and
the energy released in the fission of one uranium atom is on average 200 MeV. Find the energy consumed in MeV by
the power station in one year at 40% efficiency P = DE / Dt 1 eV = 1.6´10-19 J 1 MeV = 1.6´10-13 J Energy required in one year E = P Dt = (1/0.40)(500´106)(1)(365)(24)(60)(60)
/ (1.6´10-13) MeV DE = 2.45´1029 MeV Find the number N of uranium atoms that undergo
fission N = 2.45´1029 / 200 =
1.22´1027 atoms of uranium Find the total mass mtot of
uranium molar mass of 235U92 M = 235´10-3 kg mass of 235
atom
m
Avogadro’s number NA = 6.02´1023 M = NA
m
Mtot
= N m m = M / NA Mtot = (N / NA) M = (1.22´1027 / 6.02´1023) (235´10-3) kg
Mtot = 480 kg |