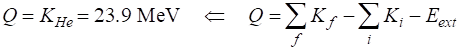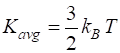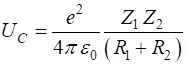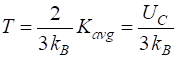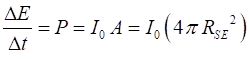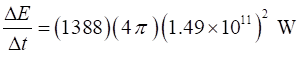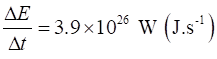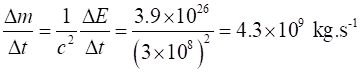|
SPECIAL RELATIVITY and NUCLEAR REACTIONS NUCLEAR FUSION |
|
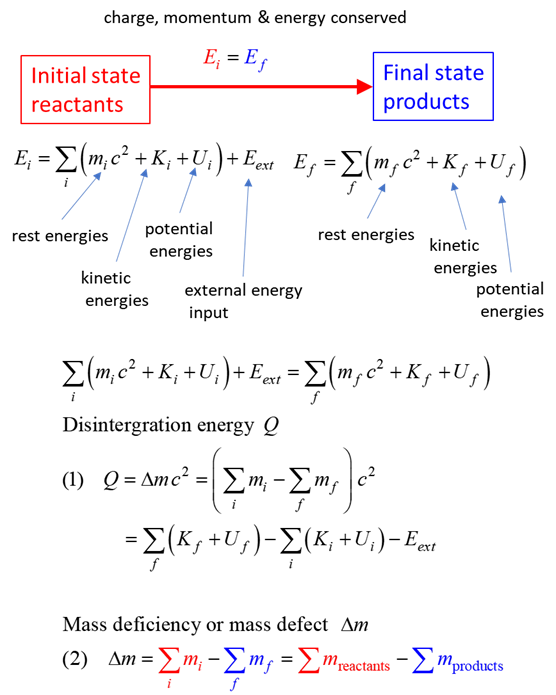
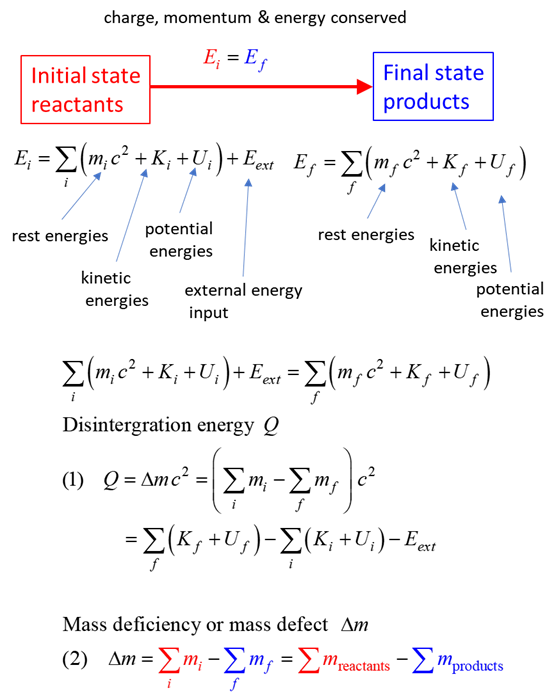
SUMMARY Total energy total
energy = rest energy + kinetic energy + potential energy
Law of
conservation mass-energy isolated
system E =
constant
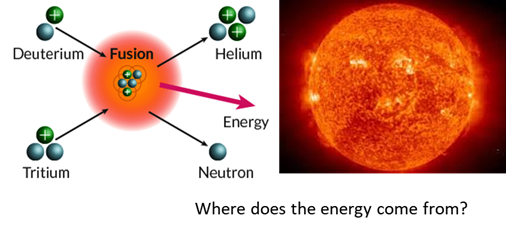
NUCLEAR FUSION Nuclear fusion is a
nuclear reaction in which multiple nuclei combine to create a single, more
massive nucleus. The resulting nucleus has a slightly smaller mass than the
sum of the masses of the original nuclei. The difference in mass is released
as kinetic energy of the products formed during the reaction according to the
Einstein equation |
|
Energy / Mass units, values and conversion factors amu (atomic mass unit) = 1 u = 1.66054´10-27 kg 1 eV = 1.602´10-19 J 1 MeV = 106 eV A mass of 1 u
(1 amu) has an energy equivalent of: E = (1.66054´10-27) (2.99792´108)2 J = 1.49242´10-10 J E = 931.494
MeV 1 u º 931.494 MeV/c2 Proton mass mp = 1.67262´10-27 kg = 1.0072765 u = 938.3 MeV/c2
Neutron mass mn = 1.67493´10-27 kg = 1.0086649 u = 939.6 MeV/c2 Electron mass me = 9.1093897´10-31 kg = 0.0005485799 u = 0.511
MeV/c2 NUCLEAR REACTIONS
NUCLEAR FUSION
In a nuclear fusion reaction, the light elements combine to produce
heavy elements. The mass of the
products is less than the mass of the reactants. The mass difference Dm is converted into kinetic energy of the products
When the primordial “BIG BANG” occurred 10-15 billion years ago, the light elements hydrogen and helium were formed in the first few minutes. It was millions of years later before the heavier elements were formed in stars and supernova explosions through nuclear fusion. It is possible to change the
structure of nuclei by bombarding them with energetic particles. Collisions
which change the identities of the target nuclei are called nuclear
reactions. The first nuclear reaction was performed by Rutherford in 1919 in
which a nitrogen target was irradiated with α-particles from a natural
radioactive source. The process of building up nuclei by
bring together individual protons and neutrons or building large nuclei by
combining small nuclei is called nuclear fusion. The mass of every stable nucleus is
less than the sum of the masses of its constituent protons and neutrons. This
mass difference is the source of energy binding the protons and neutrons
together within the nucleus. The mass of the helium isotope 4He2
is less than the combined mass of its two protons and two neutrons. Thus, if
two protons and two neutrons were to come together to form a helium nucleus
there would be a loss of mass. This loss in mass is responsible for the
release of an enormous amount of energy in this fusion process. Binding energy
of 4He2 Matlab Script mpNPBE.m
initial
state (reactants)
4He2
Atomic number Z = 2 Mass number A = 4 Number of neutrons A - Z = 2 Mass proton mP =
1.00727647 Mass neutronn mN = 1.00866492 Mass nucleus mNUC =
4.00150609
Mass defect
dm =
-0.030377 u Q-value
Q = -28.2957 u Binding energy EB = 28.2957 MeV Binding energy / nucleon EB/A = 7.0739 MeV Work needs to be done on the nucleus
to separate the protons and neutrons to become free particles at rest. This
work is equal to the binding energy EB = 28.3
MeV. So, in nuclear fusion when two light nuclei join to make one
heavy nucleus, energy will be released in the nuclear reaction. Consider
the fusion of two deuterium nuclei to from a helium nucleus.
initial state (reactants)
2H1
+ 2H1
Mass: Reactants 2.013553 u
2.013553 u
Mass: Products 4.001506 u
Mass deficiency
Disintegration energy The energy released in the fusion
reaction appears as the kinetic energy of the helium nucleus. Since Q > 0, this reaction will occur
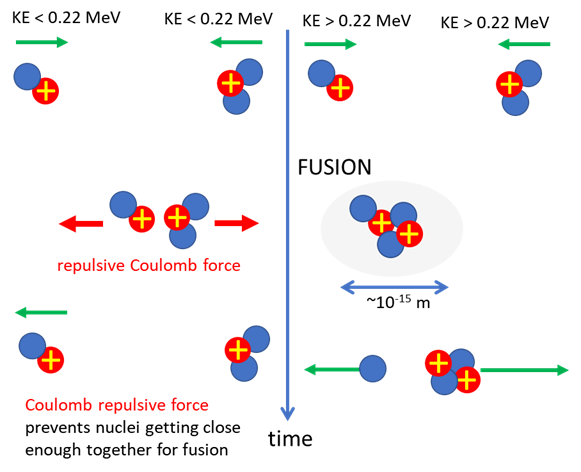
spontaneously if the two deuterium nuclei are close enough together. However, to get them close is difficult because of the
Coulomb repulsion between the two positive nuclei. TEMPERATURE FOR
FUSION Matlab Scripts mpNPreactions
mpNPCB.m To
accomplish nuclear fusion, the positively charged nuclei involved must first
overcome the electric repulsion to get close enough for the attractive
nuclear strong force to take over to fuse the particles. This requires
extremely high temperatures. We can do some simple computations to estimate
the kinetic energies of the particles and the temperature for fusion to
occur. What is the kinetic
energy of a gas at room temperature (300 K) in J and MeV? The
average translation kinetic energy At 300
K The kinetic energy of the gas
molecules is small and the gas particles could never overcome the Coulomb
barrier and fuse to produce heavier nuclei. Considering
the Coulomb barrier UC due to
the electric repulsion to be the electric potential energy of two-point
charges (with atomic numbers Z1 and Z2 and with radii R1 and R2), then the energy required to reach
a separation The
radius R of a
nucleus is approximated by the expression A
is the mass number of the nucleus Hence,
to penetrate the Coulomb barrier in a head-on collision between two
particles, the required kinetic energy and the
temperature T of the
ionized gas (plasma) is thus This
value for the temperature is an overestimate since we have used the average
temperature. In the plasma, many of the nuclei will be moving with energies much
greater than the average. The particles involved in the fusion process have a
wave nature and so can tunnel through
the barrier with an energy much lower than that given by the Coulomb barrier.
Therefore, the prerequisite for fusion is that the two nuclei be brought
close enough together for a long enough time for quantum tunnelling to act. Temperature needed
for the fusion required for the fusion of deuterium and tritium 2H1
+ 3H1
We assume that the reaction nuclei approach head-on, each with
kinetic energy K and the nuclear force comes into play when the distance between
their centres is equal to the sum of their radii. Calculation of the energy released in the fusion reaction (mpPreactions.m) Input
Reactants = [mass(1,2), mass(1,3)] ;
Products = [mass(2,4), mn ]; Output Mass: Reactants 2.013553 u
3.015501 u
Mass: Products 4.001506 u
1.008665 u
Mass defect dM
= 0.018883 u Disintergration
value Q Q = 17.589297 MeV When the reaction proceeds the
kinetic energy of the helium nuclei and neutron is 17.6 MeV. We can calculate the height of the
Coulomb barrier and the necessary temperature of the plasma for fusion using
the Script mpNPCB.m. Input %
INPUT: Z and A for the two reaction nuclei
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> %
Atomic numbers Z = [Z(1), Z(2)] Z = [1,1]; %
Mass numbers A = [A(1),A(2)] A = [2,3]; %
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Output Nuclear
radii R = 1.51 1.73 fm Coulomb
Barrier height UC = 0.44 MeV Average
kinetic energy per nuclei Kavg = 0.22 MeV Temperature T = 1.72e+09 K Very high temperatures (~ 109
K) are required for the two nuclei to get close enough together for the
strong nuclear force to act between the protons and neutrons, binding them
together. More careful calculations show that the required temperature is
about an order of magnitude less. |
|
Exercise 1 Production of energy by
the Sun The rate at which energy reaches the
Earth's surface from the Sun, is called the solar constant. Its value is approximately equal to
1388 W.m-2. Use the values of the solar constant and the distance
between the Earth and Sun to estimate the rate at which energy is emitted by
the Sun and the corresponding decrease in the Sun’s mass.
Solution Assume that the Sun radiates
uniformly in all direction. The energy emitted from the Sun passes through a
spherical surface area A of
radius The rate P at which
the energy passes this spherical surface is Therefore, the rate at which energy is radiated from the Sun is
The corresponding rate of decrease
in mass of the Sun is The loss in mass of the Sun is
equivalent to three times the mass of the Queen Mary every second.
The Sun loses a rather a large
amount of energy each second. Since the mass of the Sun is 1.99x1030
kg, the loss in mass each year is small. Even after 1.5x109 years
(1.5 billion years), radiating at its present rate, the Sun would lose a mere
0.01% of its mass. The Sun will not evaporate away in our lifetime. |
|
Proton-Proton Cycle A useful
link to proton-proton cycle which is one of the main fusion processes for producing
energy by our Sun http://burro.astr.cwru.edu/Academics/Astr221/StarPhys/ppchain.html The main source of energy for
stars is the “burning” of hydrogen to form helium. The main
sequence of fusion reactions for four hydrogen atoms to combine to form
helium is called the proton-proton cycle. It
is easy to calculate the Q-value for each
reaction with the Matlab Script mpNPreactions.m. 1H1
+ 1H1
Reactants = [
mass(1,1) mass(1,1) ] ; Products = [ mass(1,2) me ]; Mass:
Reactants 1.007276 u
1.007276 u
Mass:
Products 2.013553 u
0.000549 u
Mass
defect dM
= 0.000451 u Disintegration
value Q Q = 0.420222 MeV 1H1
+ 2H1
Reactants = [ mass(1,1)
mass(1,2) ] ; Products = [ mass(2,3) ]; Mass:
Reactants 1.007276 u
2.013553 u
Mass:
Products 3.014932 u
Mass
defect dM
= 0.005897 u Disintegration
value Q Q = 5.493477 MeV
3He2 + 3He2 Reactants = [ mass(2,3)
mass(2,3) ] ; Products = [ mass(2,4) mass(1,1) mass(1,1) ]; Mass: Reactants 3.014932 u
3.014932 u
Mass: Products 4.001506 u
1.007276 u
1.007276 u
Mass defect dM
= 0.013805 u Disintegration value Q Q = 12.859576
MeV The net result of the proton-proton cycle is that four protons
combine to form one 4He2 nucleus plus two positrons two
neutrinos and two gamma rays (it takes two of each of the first two reactions
to produce the two 3He2 for the third reaction) 2(1H1
+ 1H1)
2(1H1
+ 2H1)
3He2
+ 3He2
4(1H1
) The
total energy released for the net reaction is 24.38 MeV. But, the two
positrons (reaction 1) will quickly annihilate with two electrons to release
more energy { 2(2mec2) = = 2.04 MeV }. So, the total energy
released is 26.75 MeV. Reaction 1
which produces the deuterium 2H1 has a very low
probability and thus occurs very infrequently and this limits the rate at
which the Sun produces energy. CNO Cycle (Carbon-12 Cycle) In stars
that are more massive than the Sun, it is more likely that the energy output
comes principally from the CNO (carbon)
cycle. One possible sequence of the CNO cycle is The two
positrons will annihilate with two electrons releasing a further 2.04 MeV.
So, the total energy released in the CNO cycle is 26.74 MeV. All the values were calculated with the Script mpNPreactions.m. LIFETIME OF OUR SUN mpNPsun.m We can do an
amazing calculation to estimate the lifetime of our Sun. Only the core of the Sun is hot
enough for nuclear fusion to occur via the proton-proton cycle. So, we can
estimate the amount of available energy from the Sun’s core to sustain
the Sun over its lifetime using the following numerical data. Average density of
Sun’s core
Mass of a proton
Radius of Sun
Radius of Sun’s core
Q-value for proton-proton cycle
Sun-Earth distance
Solar constant (solar radiation reaching Earth)
Proportion of core hot enough to sustain nuclear fusion
We can now calculate the following:
Energy output of the Sun per year
Radius of core
Volume of Sun’s core
Mass of Sun’s Core
Number of proton’s in Sun’s core Available energy from core by fusion of 4 protons to give helium
Lifetime of Sun in years Results of the computation: Qcore = 1.98x1044 J ESun = 1.21x1034 J/y LifeTime = 1.6x1010 y We get a remarkable result for such
a simple computation. The Sun can radiate energy for 1010 years
as a main sequence star. The fusion of four protons to form helium does not
release much energy, but when you consider the tremendous number of protons
that can undergo fusion, the Sun’s lifetime is very long and is in the
order of 10 billion years. |