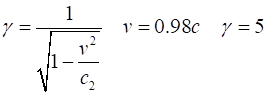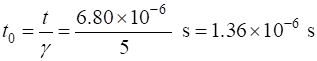|
Does Einstein's theory of special
relativity accurately describe the motion of objects traveling close to the
speed of light?
The theory of special relativity has made
many astonishing predictions. Einstein did not receive his Noble Prize for
his theory of special relativity but for a minor contribution to our
understanding of science – the photoelectric effect. Scientist at the
time, were uncertain of Einstein’s predictions as they were so
inconceivable and so against long-held believes. For more than a century,
experiments have been carried out to test Einstein’s theories. So far,
all experimental evidence has been confirmed the predictions of special
relativity and general relativity.
Muons are unstable
particles with a rest mass of 207 times that of an electron and a charge of
±1.6x10-19 C.
Muons decay into electrons or positrons with an average lifetime of
2.2 ms as measured in their inertial frame of reference.
When
high energy particles called cosmic rays (such as
protons) enter the atmosphere from outer space, they interact with air
molecules in the upper atmosphere at a height of about h = 10 km above the Earth’s
surface creating a cosmic ray shower of particles including muons that reach
the Earth’s surface. The muons are created in these
cosmic ray showers travel at  w.r.t to the Earth. In a stationary
frame of reference, on average a muon exists for about w.r.t to the Earth. In a stationary
frame of reference, on average a muon exists for about 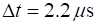 before it
decays into other particles. before it
decays into other particles.
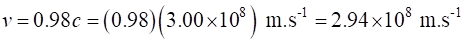
relativity factor 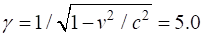
Newtonian (classical) point of view
We can apply the principles of classical physics to calculate
the distance a muon on average will travel before it decays (figure 1)

Fig. 1. On average a muon will travel 650 m before decaying. So,
in terms of classical physics, very few muons
should be able to reach the surface of the Earth. 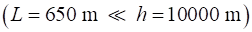
Hence, from a Newtonian point of view, there is a low
probability of a muon reaching the Earth’s
surface from the upper atmosphere where they are produced. However,
experiments show that many muons do reach the Earth’s surface in cosmic
ray showers.
Special
relativity: muon frame of reference
In the frame of reference of the muon, the Earth is approaching
at speed  and the distance to the Earth as measured in the muon’s
frame is the contracted length (figure 2) and the distance to the Earth as measured in the muon’s
frame is the contracted length (figure 2)
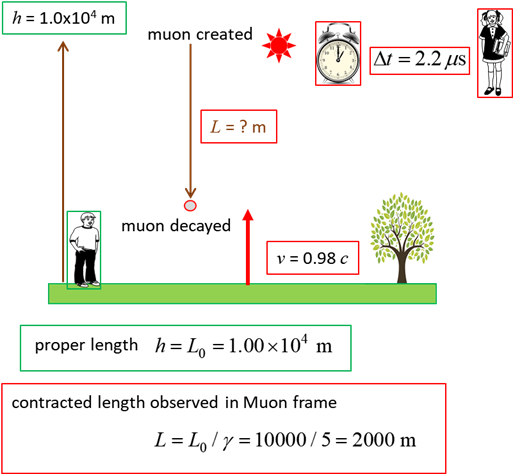
Fig. 2. Using
the principle of length contraction, the muons
travel on average a much greater distance compared with the classical prediction 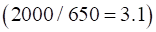 . .
The contracted distance is much less and so many muons will be
able to reach the Earth’s surface as 2000 m >> 650 m.
Special relativity: Earth frame of reference
The observer on Earth needs two clocks to measure the time
interval for the muon to decay. The time interval  corresponds to the dilated time interval whereas the proper time
interval corresponds to the dilated time interval whereas the proper time
interval 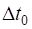 is the average lifetime in the
muon’s frame (figure 3). is the average lifetime in the
muon’s frame (figure 3).
Fig. 3. Frame of
reference is the Earth. The Earth observer measures the dilated time
interval, hence will conclude the muon will travel much further than that
given by the classical prediction.
The
average distance travelled is now long enough for many muons
to reach the Earth’s surface.
Another look at
muon decay
The decay of muon can
be accurately described by the radioactive decay law
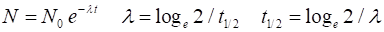
where 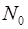 and and  are the
number of detected muons at times are the
number of detected muons at times 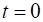 and time
t respectively. and time
t respectively.
 is the
half-life (time for the number of muons detected to halve) and is the
half-life (time for the number of muons detected to halve) and 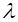 is the
decay constant. The measured half-life and decay constant for muons at rest
in the laboratory are is the
decay constant. The measured half-life and decay constant for muons at rest
in the laboratory are
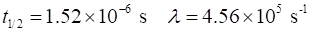
An
experiment was performed by placing a Geiger counter to detect muons on the
top of a mountain 2000 m high. The muons are assumed to be moving at a speed
equal to 0.98c. In a time interval T the Geiger counted 1000 muons. The
Geiger counter was moved to the bottom of the mountain, 2000 m below the
peak. In the same time interval T, the Geiger counter registered 540
muons. These are the muons that survived the trip without decaying.
Classically,
we can calculate the number of muons surviving the trip.
distance
travelled by muons 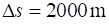
speed of muons 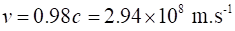
time interval for trip

Number
of surviving muons

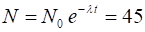
So, only 45 muons should survive the trip. Something is wrong !!!
Our classical
theory predicts 45 muons, but measurements record 540 muons. The problem must
be approached using special relativity. The muons are moving at a speed of
0.98c w.r.t the Earth. So, we must consider the time dilation effect.
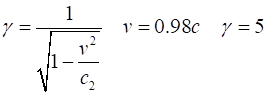
The Earth
based clock records a time interval of 6.80x10-6 s for the muon to
travel from the top to the bottom of the mountain.
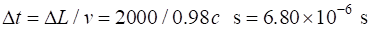
The Earth
based observes see the muon’s “moving clock” record the
proper time 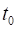

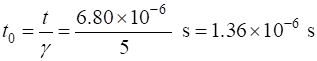
In the
muon’s rest frame, the decay of the muon is given the radioactive decay
law is
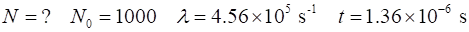
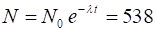
The number
of muons surviving the trip is 538, which agrees with observations. An
experiment like this was performed by B. Rossi and D. Hall in 1941 at Mount
Washington, New Hampshire, U.S.A. Their results agreed with the predictions
of special relativity and not the predictions of classical physics.
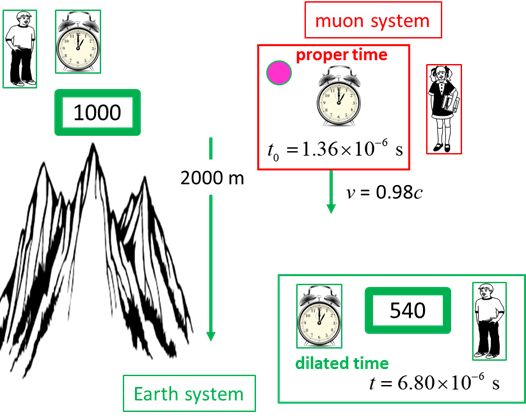
Fig.
4. The number of muons
detected at the top of the mountain is 1000 whereas at the bottom of the
mountain only 540 survived without decaying. The experimental result agrees
with the prediction based on the time dilation equation.
|