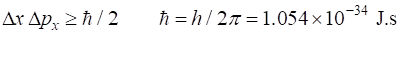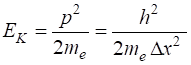VISUAL PHYSICS ONLINE

 

8.1 FROM THE UNIVERSE TO THE ATOM

WHY DO ATOMS EXIST?

OUR MYSTERIOUS QUANTUM UNIVERSE

 

Have you ever thought about why our universe exists as it does, and that the building blocks of just about everything is made of atoms. Our model of an atom is that is made of a positive nucleus and surrounded by negative electrons. But common sense and the laws of classical physics tells us that a negative object is attracted to a positive object. So, the negative electrons should just rush and collapse into the nucleus atoms should not exist, and the world we live in would not be as we know it !!!

 

We can only explain the existence of our universe and that atoms are real using the very strange ideas of quantum physics.

 

Do you know what a wave is and what is a particle?

 

But, what about an electron? Is it a particle or a wave? The strange answer is that is not a classical particle or a classical wave. The electron exhibits both particle-like and wave-like behaviour but it is not a classical particle or a classical wave.

 

So, we dont know what an electron is and cant use a picture to represent it. However, the behaviour of electrons can be described extremely accurately using the mathematics of quantum mechanics where predictions of their behaviour are expressed in terms of probabilities. Hence, it is not possible to predict exactly what will happen in any circumstance. For example, we cant predict when an excited atom will emit light or do we know when a given radioactive nucleus will decay. So, what happens can only be described statistically.

 

 

Quantum mechanics has many aspects. For example, the idea that a particle has a definite location and a definite speed is no longer allowed it is wrong. An important principle of quantum mechanics is called the Heisenberg Uncertainty Principle that says that one cannot know where something is and how fast it is moving at any instance of time. One way of expressing this principle is

where is the uncertainty in the position along the X direction in which the particle is moving with momentum and is the uncertainty in the X momentum. This rule is the explanation of a very mysterious paradox: if the atoms are made from positive and negative charges, why dont the negative charges simply sit on top of the positive charges since they attract each other and get so close as to completely cancel each other out?

 

Why are atoms so big?

Why is the nucleus so small, so massive and at the centre of the atom with the electrons around it?

Size of an atom ~ 10-10 m

Size of nucleus ~ 10-15 m

Volume of atom / volume nucleus ~ 1015 (an atom is really big compare with nucleus)

What keeps the electrons from falling into the nucleus?

 

If an electron was within the nucleus, then we would know its position very accurately . Then, the uncertainty principle would require that the electron would have large uncertainty in momentum and hence a large value for its momentum and kinetic energy . With this energy, the electron would break away from the nucleus. Hence, the electron cannot exist with a nucleus.

 

Therefore, the uncertainty principle contains implications about the energy that would be required to contain a particle within a given volume. The value of Planck's constant h, appearing in the uncertainty principle, determines the size of the confinement that can be produced by the fundamental forces of nature. The following very approximate calculation serves to give an order of magnitude for the energies required to contain electrons within an atom and nucleus.

 

Energy to contain an electron with an atom

Assume:

Location

Momentum

Kinetic energy

Uncertainty principle

So, binding energies of electrons in atoms and energies involved in chemical reaction are in the order of a few electron volts.

 

Energy to contain an electron with a nucleus

Assume:

Location

Momentum

Kinetic energy

Uncertainty principle

The energy to confine an electron to the nucleus is more than a thousand greater than the energies observed in nuclear processes. So, electrons cannot be confined within a nucleus.

 

If you repeat the calculation for a proton confined to a nucleus you get a result of the confinement energy of 2 MeV. Energies observed for nuclear processes are in the order of a few MeV. Hence, protons and neutrons can be confined with the small volume of a nucleus by the strong nuclear force.