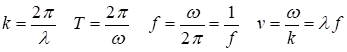|
WORKSHOP ACTIVITY pa31_ttw TRAVELLLING
TRANSVERSE WAVES
[1D] TRAVELLING
HARMONIC WAVE A [1D]
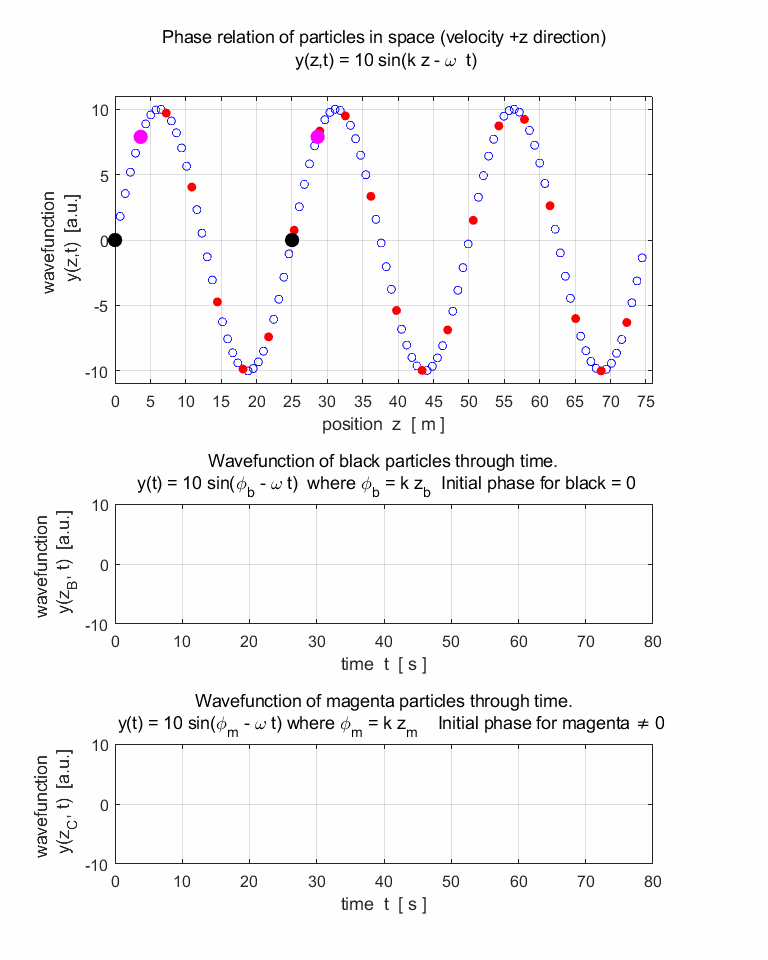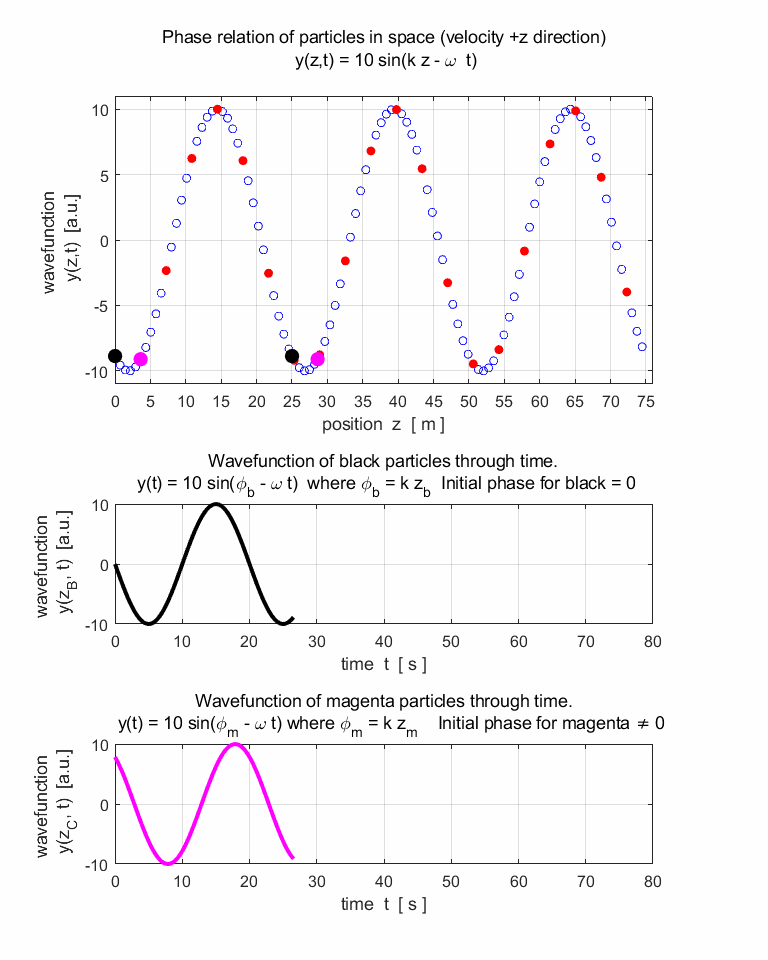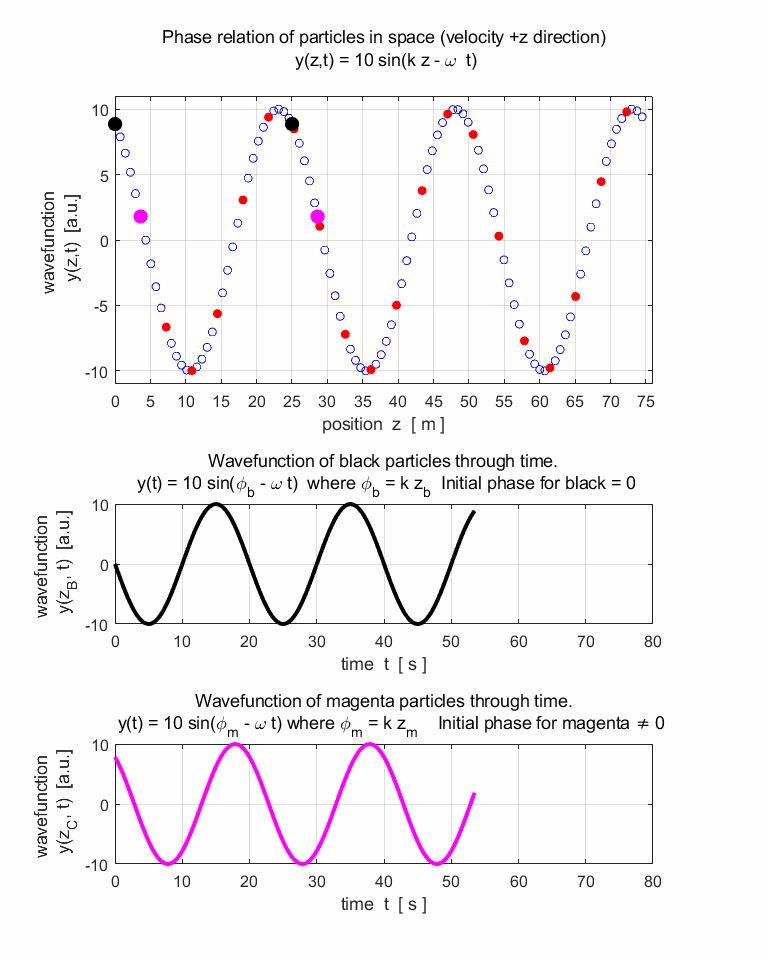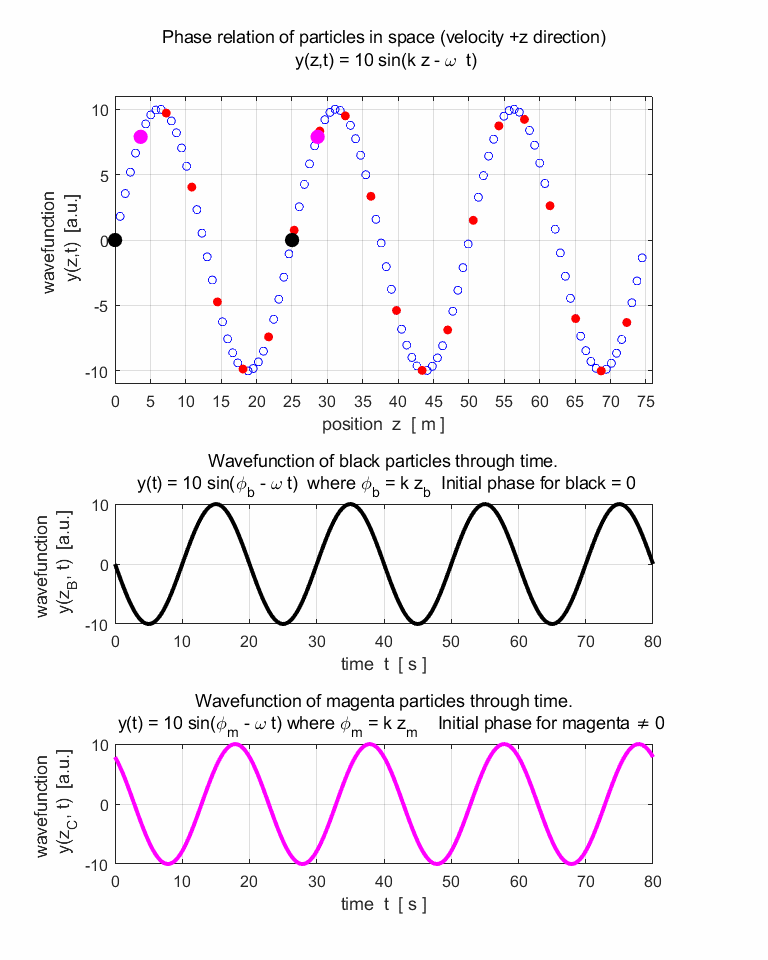
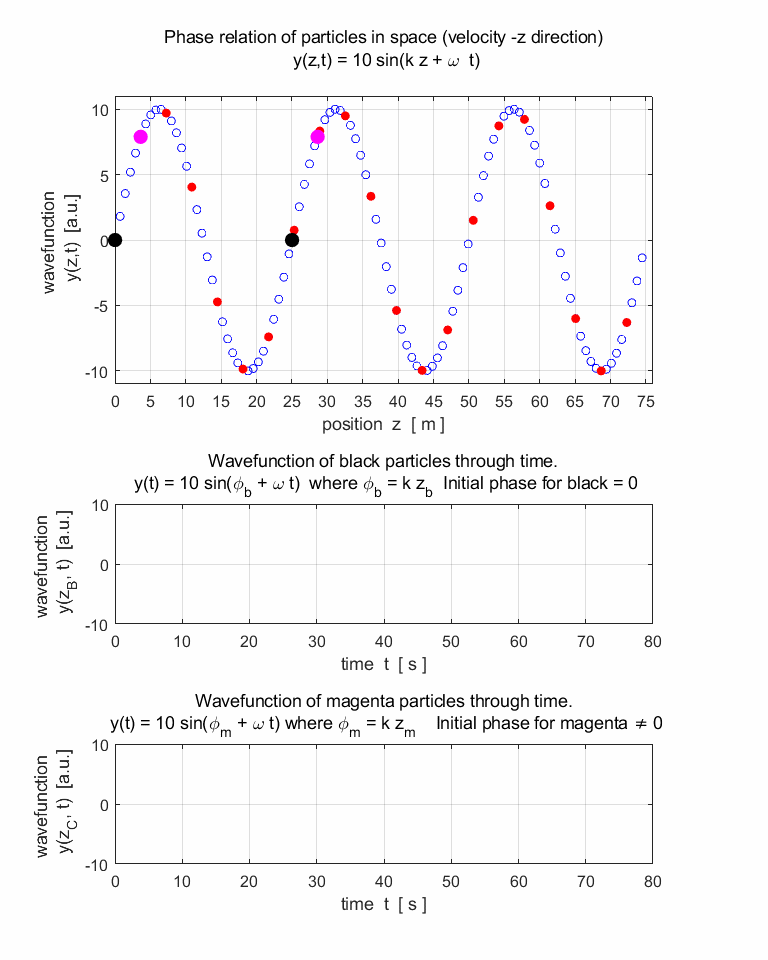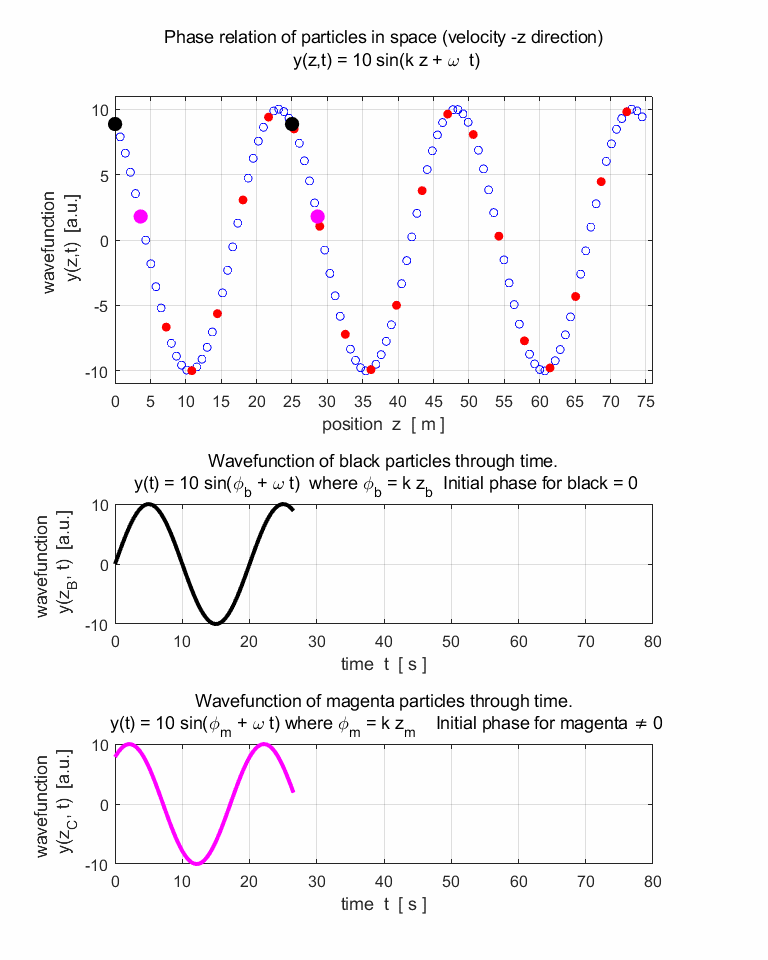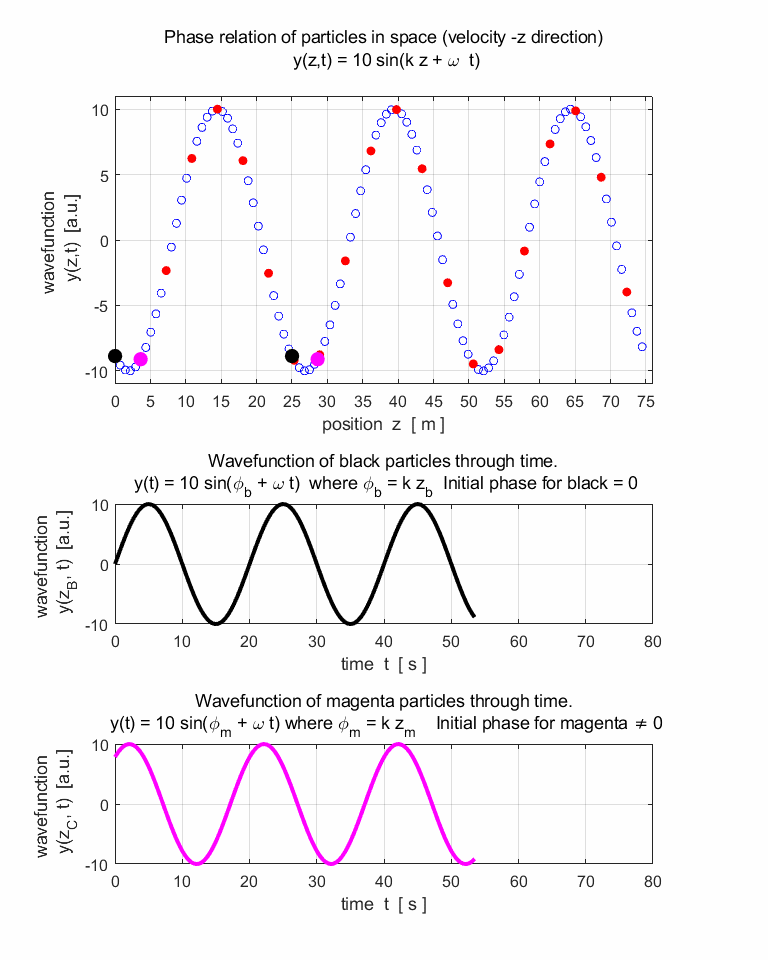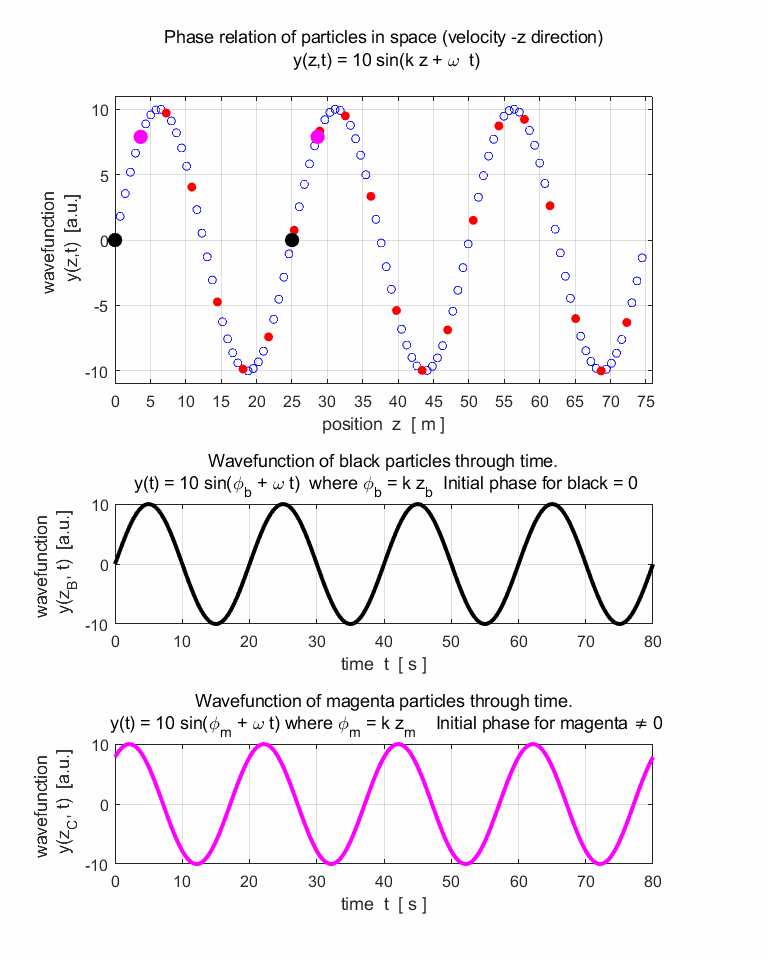
travelling harmonic wave can be represented by the wavefunction y(z,t) that is periodic both
in space (z) and time (t). The profile
of the travelling wave is sinusoidal at any instant and each point in the
track of the wave performs simple harmonic motion. The wave function y(z,t) is given by equation 1. (1) (2) where A is the amplitude, k is the propagation
constant (or wave number), It is not
possible to draw a simple graph of the wavefunction given by equation 1. So,
animations of travelling waves can play a very important role to help improve
ones understanding of the mathematical description of travelling waves. Carefully
view the animations below and answer the questions to test your understanding
of some of the fundamental concepts of wave motion. You can also
download the animations as avi files so that you
can stop and start the animations in your media player.
Propagation to the left (+ Z direction) avi_TW_LR.avi
Propagation to the right (-Z direction) avi_TW_RL.avi |
|
|
|
|
|
Questions 1.
What is the amplitude of the wave? 2.
Why does one wave travel to the left and in the other
animation, the wave travel to the right? 3.
Describe in your own words, the meaning of the term wavelength.
Estimate the numerical value of the wavelength. 4.
Describe in your own words, the meaning of the term period.
Estimate the numerical value of the period. 5.
Describe in your own words, the meaning of the term frequency.
How does the term relate to the motion of the black particles? Estimate the
numerical value of the frequency. 6.
Calculate the values of the propagation constant k
and angular
frequency 7.
How far does the crest of the wave advance in a time
interval of 1 period? Describe in your own words, the meaning of the term wave velocity.
Estimate the numerical value of the wave velocity. 8.
Look at the motion of the black and magenta particles. When
are the particles stationary? When are the particles moving with maximum
speed? Describe their motion and state the meaning of the term particle
velocity. 9.
In your own words, what conclusions can be made about the
wave velocity and particle velocities. 10. Why do we say that the two black particles
vibrate in-phase while the black and magenta particles vibrate out-of-phase? 11. What is the separation between the two
black or magenta particles in terms of distance (wavelength) and phase (phase
angle measured in radians)? |
|
The animations were produced using Matlab. wm_ttw.m An animation
of a one-dimensional travelling wave is displayed. The animation can be saved
as an animated gif
file or as a avi
file by setting the value the parameter flagA. The
saved animated gif files and avi files can be used
for display purposes and embedded in html documents. The advantage of the avi files is the animations can be repeatedly stopped and
restarted. The program was written by John Sims (Biomedical
Engineering Department, Universidade Federal do
ABC, Brasil) and Ian Cooper. Download
Matlab mscripts Directory |