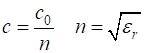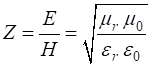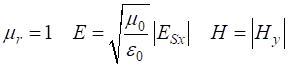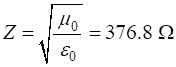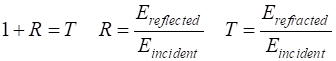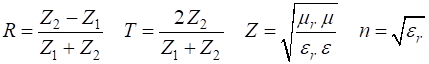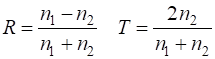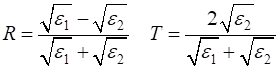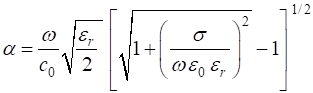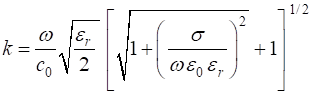|
[1D] FDTD
electromagnetic wave simulations of propagating waves in non-magnetic and
lossy dielectric media Ian Cooper Please
email any corrections, comments, suggestions or additions matlabvisualphysics@gmail.com View ELECTROMAGNETISM USING THE FDTD METHOD ft_03.m Download and run the script ft_03 .m. Carefully inspect the script to see how the FDTD method is implemented. Many variables can be changed throughout the script, for example, type of excitation signal, boundary conditions, time scales, properties of the medium. We can also model the propagation of EM waves in materials where the loss term is specified by the conductivity of the material. This loss term results in the attenuation of the propagating energy. A wave encountering a boundary between media with different refractive indices (relative permittivities) will in general be partially refracted (transmitted) and partially reflected at the boundary. The relationship between the incident wave and the refracted and reflected waves can be expressed in terms of the transmission T and reflection R coefficients. This relationship can be expressed in terms of impedances Z or refractive indices n. For a
non-magnetic and non-lossy dielectric medium, the speed of propagation c
of an electromagnetic wave depends on the refraction index n of
the medium. The refractive index n is a function of
the relative permittivity
For an
electromagnetic wave the impedance Z is defined as the
ratio between the magnitudes of the E and H
fields. For a medium with dielectric constant
The
impedance of free space is For our [1D] model of the incident wave reaching the boundary, we must have and In the
case of non-magnetic material The amplitude for the electric field propagating in the +Z direction in a lossy dielectric medium is given by The two parameters and are given by
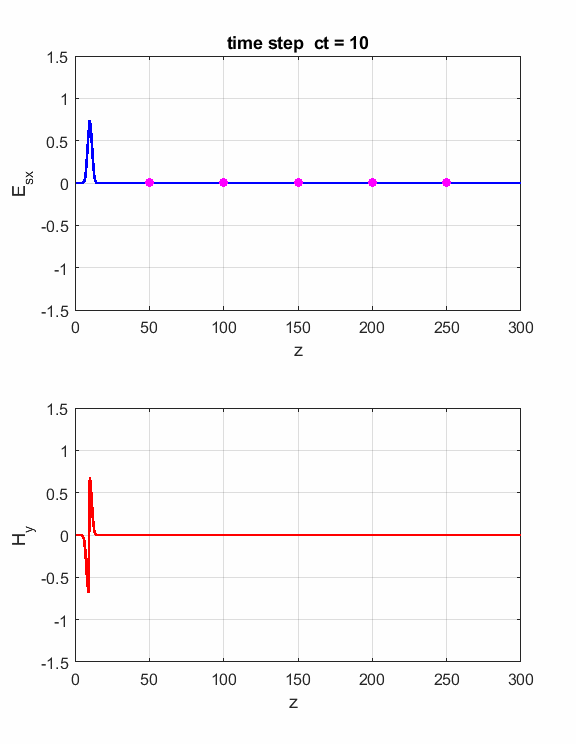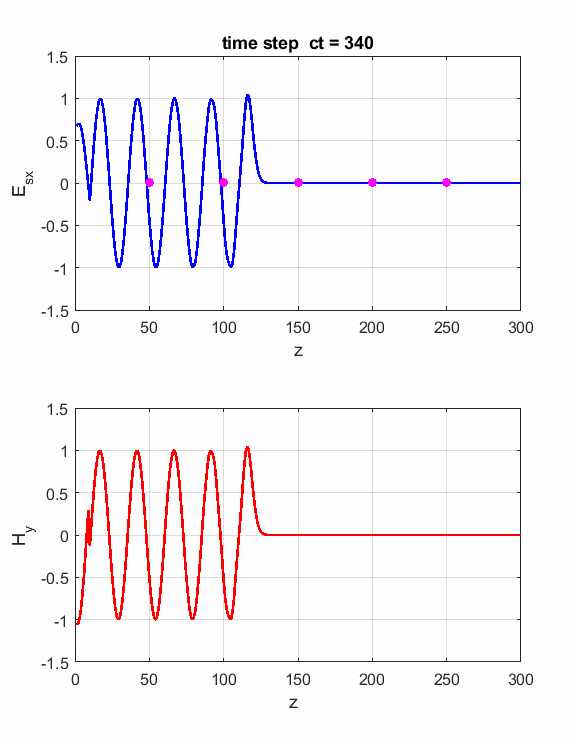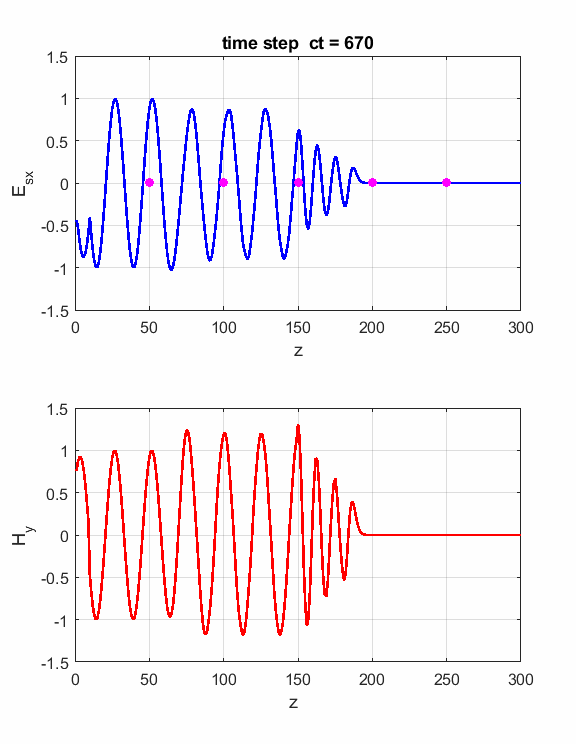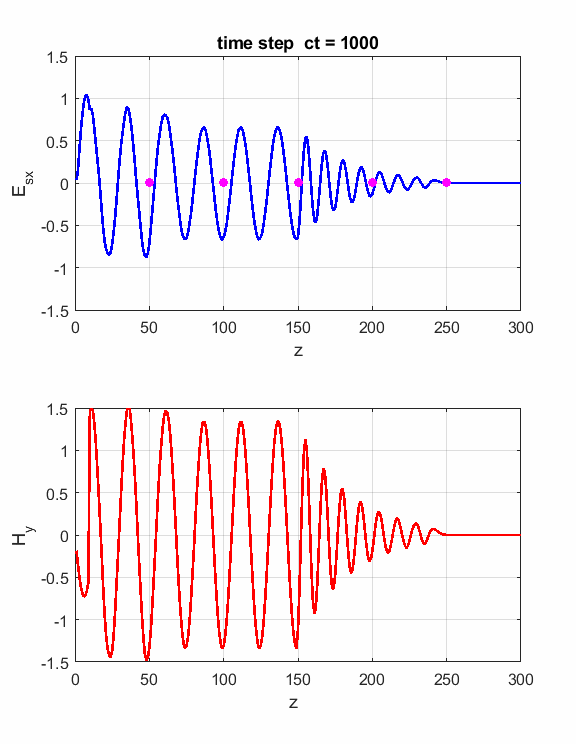
Simulations Parameters: Nt = 1000 Nz = 300 lambda = 3x108/(400x106) (f = 400 MHz) eR1 = 1 S = 0 S2 = 0.01 zS = 150
Fig. 1. Animation of sinusoidal EM wave striking a lossy dielectric medium
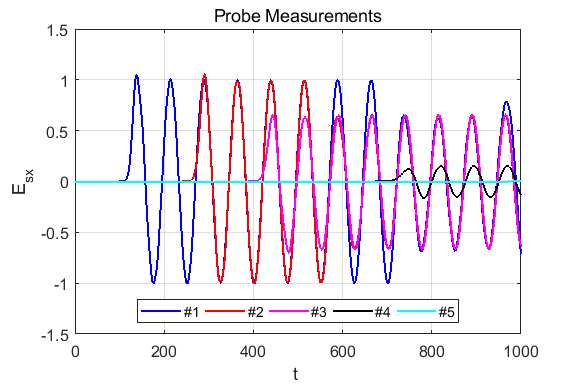
Fig. 2. Probes measurements of electric field.
Fig. 3. Figure Window summary of results. There is reasonable agreement between the theoretical predictions and the values calculated from the exponential decay of the EM wave in the lossy dielectric medium. |