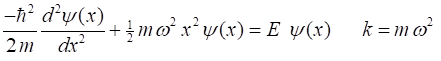DOING PHYSICS WITH MATLAB

MATLAB RESOURCES

INTRODUCTION TO QUANTUM MECHANICS

3rd Edition

David J Griffiths & Darrel F Schroeter

                  

Ian Cooper

matlabvisualphysics@gmail.com

 

 

CHAPTER 2

THE SCHRODINGER EQUATION

THE HARMONIC OSCILLATOR

HERMITE POLYNOMIALS

 

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

   GitHub

   Google Drive

 

QMG23C.m

 

Griffith in section 2.3.2 used an analytically method to solve the Schrodinger equation which uses Hermite polynomials. Again, much mathematics and little physics. With software such as Matlab and fast computers with lots of memory, a better approach is to use numerical methods.

 

I will consider the truncated parabolic potential discussed in the previous chapter.

https://d-arora.github.io/Doing-Physics-With-Matlab/mpDocs/QMG2D.htm

 

The Schrodinger equation for the harmonic oscillator is

      

    

 

The normalized solution of the Schrodinger equation given by Griffiths is

  

 

where the scaled position is   and  are the Hermite polynomials.

 

The Script QMG23C.m can be used to investigate the analytical solution in more detail than is given in Griffiths’ text.

 

The Matlab function hermiteH(n,x) is used to evaluate the Hermite polynomial. For example, to calculate the first 5 orders and plot the results:

 

% Hermite polynomials =============================================

   NP = 5;

   Hn = zeros(NX,NP);

   xH = linspace(-2,2,NX);

   for c = 1:NP

     Hn(:,c) = hermiteH(c-1,xH);

   End

 

 

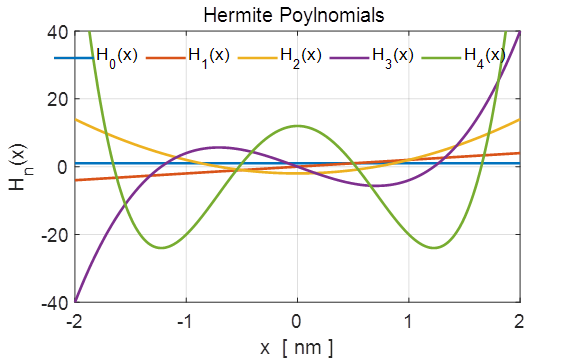
Fig. 1.   The first 5 Hermite polynomials n = 0, 1, 2, 3 and 4.

 

The parabolic potential energy function is defined in terms of  and .

        

           

 

Position is generally measured in nanometres (nm) and energy in electron volts (eV) for an electron bound in the parabolic well.

 

Results of the simulation for the electron trapped in the parabolic well are displayed graphically.

 

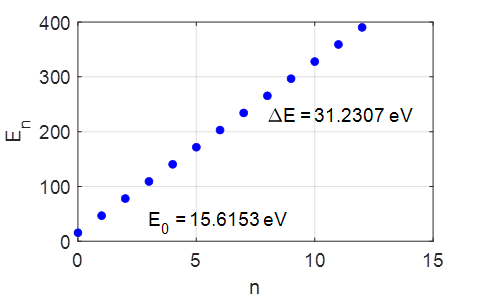
Fig. 2.  The first 6 total energy levels for the harmonic oscillator.

 

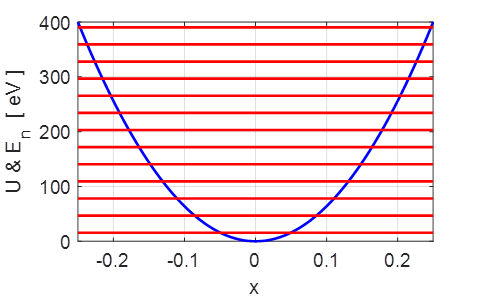
The quantized energy levels are given by . The ground state energy level is E0= 15.6153 eV and the energy levels are equally spaced with  = 31.2207 eV.

Fig. 3.    The potential energy function and the quantized energy levels. Note: the energy levels are equally spaced, the separation between adjacent levels being  and the zero-point energy is .

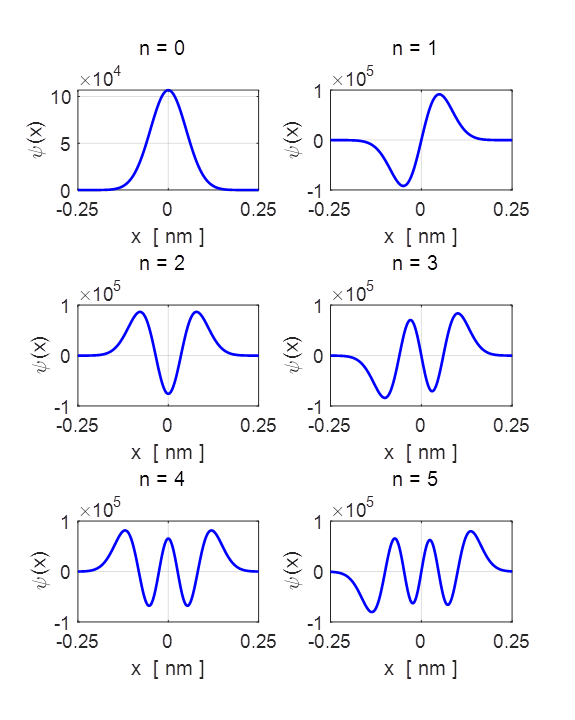
Fig. 4.  The first 6 eigenfunctions or stationary states of the harmonic oscillator.

 

From figure 4, it is clear that  is an even function  when n is even and an odd function  when n is odd. Such symmetry is typical of stationary wave (standing wave) eigenfunctions arising from a symmetrical potential energy function: the functions have alternate even and odd symmetry relative to a reflection about the equilibrium position. These functions are said to exhibit even and odd parity according as they are even or odd.

Fig. 5. The potential energy U, kinetic energy K and total energy E for the stationary state n = 2 (top) and the wavefunction (bottom).

 

 

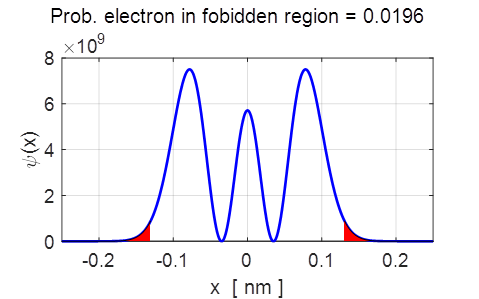
Fig. 6.   The probability density for the stationary state n = 2. The red coloured areas represent the classically forbidden region.

 

 

In the region –0.13 < x < 0.13 (between the vertical blue lines) the kinetic is positive, outside this region the kinetic energy is negative and is called the classical forbidden region, since a classical particle could not move into this forbidden region where the kinetic energy is negative. However, the probability of locating the particle in the forbidden region is not zero as the wavefunction penetrates this classically forbidden region. It is immediately obvious that the probabilities obtained classically and quantum mechanically are very different. According to the classical view of the harmonic oscillator, the probability of finding the particle is greatest near the limits of oscillation and there is zero probability that the particle is beyond those limits. According to quantum mechanics, the highest probability of locating the particle is not at the limits and may even occur at the equilibrium position and there is a small but non-zero probability of finding the particle beyond the limits of oscillation. For the stationary state n = 2, on making repeated measurements on identical systems, the probability of locating the electron in the classically forbidden area is about 2% which is not an insignificant number.