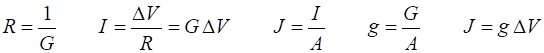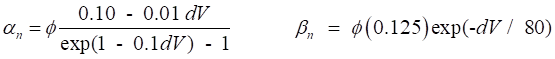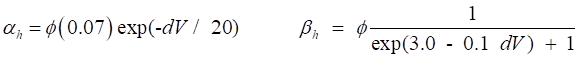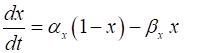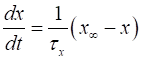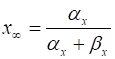DOING PHYSICS WITH MATLAB

COMPUTATIONAL NEUROSCIENCE

THE NEURON MEMBRANE: ION CHANNELS AND GATE VARIABLES

Ian Cooper

Any comments, suggestions or corrections, please email me at

matlabvisualphysics@gmail.com

MATLAB

Download Directory

npHHA.m bp_neuron_02.m npIC.m

INTRODUCTION

The equations of Hodgkin and Huxley provide a good description of the electrophysiological properties of the giant axon of the squid. These equations capture the essence of spike generation by sodium and potassium ion channels. The basic mechanism of generating action potentials is a short in influx of sodium ions that is followed by an efflux of potassium ions. Cortical neurons in vertebrates, however, exhibit a much richer repertoire of electrophysiological properties than the squid axon studied by Hodgkin and Huxley. These properties are mostly due to a larger variety of different ion channels.

In biophysically based neural modelling, the electrical properties of a neuron are represented in terms of an electrical equivalent circuit. Capacitors are used to model the charge storage capacity of the membranes (a semipermeable cell membrane separates the interior of the cell from the extracellular liquid and acts as a capacitor). 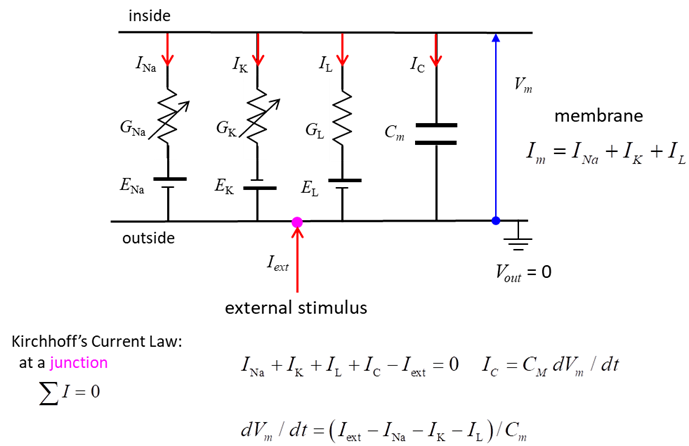Resistors are used to model the various types of ion channels embedded in the membrane, and batteries are used to represent the electrochemical potentials established by differing intracellular and extracellular ion concentrations. Figure 1 shows the equivalent circuit used by Hodgkin and Huxley in modelling a segment of squid giant axon. The current across the membrane has two major components, one associated with the membrane capacitance and one associated with the flow of ions through resistive membrane channels. They found three different types of ion currents: Na⁺, K⁺, and a leak current that consists mainly of Cl^- ions. The flow of ions through a cell membrane of a neuron is controlled by special voltage dependent ion channels: Na⁺ ion channel, K⁺ ion channel and a leak ion channel for all other ions. The neuron can be stimulated by an external current I_ext injected into the interior of the neuron.

Fig.1. Hodgkin – Huxley model: Electrical equivalent circuit for a short segment of squid giant axon. Capacitor (capacitance C_m of the cell membrane); Variable resistors (voltage-dependent Na⁺ and K⁺ conductances G_Na, G_K ); fixed resistor (voltage-independent leakage conductance G_L); Batteries (reversal potentials Na⁺, K⁺ , leakage: E_Na, E_K, E_L); Membrane potential V = V_m = V_in - V_out; External stimulus I_ext; Current directions (arrows: I_ext outside ® inside (I < 0), I_Na, I_K and I_L inside ® outside (I > 0).

Electrical potential (voltage) DV, current I (area A, current density J), resistance R and conductance G are related by the equations

Electrical activity in neurons is sustained and propagated by ion currents through neuron membranes as shown in figure 1. Most of these transmembrane currents involve four ionic species: sodium Na⁺, potassium K⁺, calcium Ca²⁺ and chloride (Cl^-). The concentrations of these ions are different on the inside and outside of a cell. This creates the electrochemical gradients which are the major driving forces of neural activity. The extracellular medium has high concentration of Na⁺ and Cl^- and a relatively high concentration of Ca²⁺. The intracellular medium has high concentration of K⁺ and negatively charged large molecules A^-. The cell membrane has large protein molecules forming ion channels through which ions (but not A^-) can flow according to their electrochemical gradients.

The concentration asymmetry is maintained through

· Passive redistribution: The impermeable anions A^- attract more K⁺ into the cell and repel more Cl^- out of the cell.

· Active transport: Ions are pumped in and out of the cell by ionic pumps. For example, the Na⁺/K⁺ pump, which pumps out three Na⁺ ions for every two K⁺ ions pumped.

In the Hodgkin – Huxley model only the movement of the sodium, potassium ions are considered, all other ions are considered as part of the leak current.

ION CHANNELS

In this section we give an overview of some of the ion channels encountered in different neurons. The basic equation of detailed neuron models is more or less the same as that of the Hodgkin-Huxley model except that it contains more types of ion channels. The membrane potential V_m of a neuron is given by

(1)

where c_m is the membrane capacity per unit area, J_ext is the synaptic input current density, and J_c is the current density through ion channel c. As in the Hodgkin-Huxley model, sodium and potassium currents are described by equations of the form

(2)

where is the maximum conductance of ion channel c, E_c is the reversal potential for ion c, and k and h are activation and inactivation variables, respectively. The exponents p and q are integer parameters representing the number of gates for ion channel c (figure 3).

(3)

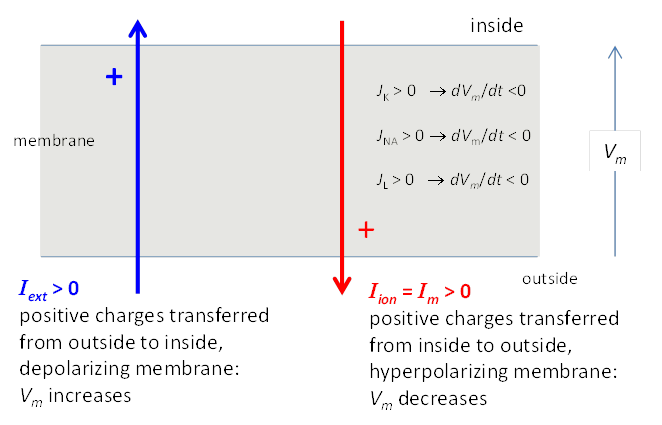
Fig. 2. Sign convention for currents. A positive external current I_ext (outside to inside) will tend to depolarize the cell (i.e., make V_m more positive) while a positive ionic current I_ion will tend to hyperpolarize the cell (i.e., make V = V_m more negative).

In a simple model, the Na⁺ and K⁺ ions are considered to flow through ion channels where a series of gates determine the conductance of the ion channel. The macroscopic conductances of the Hodgkin & Huxley model arise from the combined effects of a large number of microscopic ion channels embedded in the membrane. 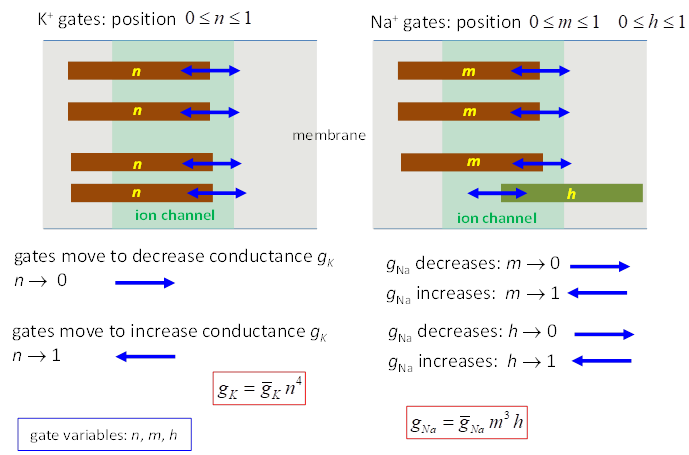Each individual ion channel can be thought of as containing one or more physical gates that regulate the flow of ions through the channel. The variation in g values is determined by the set of gate variables k and h and the number of gates p and q

An activation gate k ® conductance increases with depolarization

An inactivation gate h ® conductance decreases with depolarization

The Na⁺ channel is controlled by 3 activation gates and 1 inactivation gate

The K⁺ channel is controlled by 4n activation gates

The value of the conductance g depends upon the membrane voltage V_m because the values of n, m and h depend on time, their previous value at an earlier time and the membrane potential. The resting membrane potential is given by the symbols V_rest or V_r.

Fig. 3. Ion channels and gate variables for Na⁺ and K⁺.

The rates of change of the gate variables are described by the equations

(4)

where the ’s and ’s are rate constants

rate of closed gates opening rate of open gates closing

fraction of gates opening per second

fraction of gates closing per second

The various functions for and are empirical functions of V_m that have been adjusted by Hodgkin and Huxley to fit the data of the giant axon of the squid. Note: The gain function of the Hodgkin-Huxley model is discontinuous at the firing threshold.

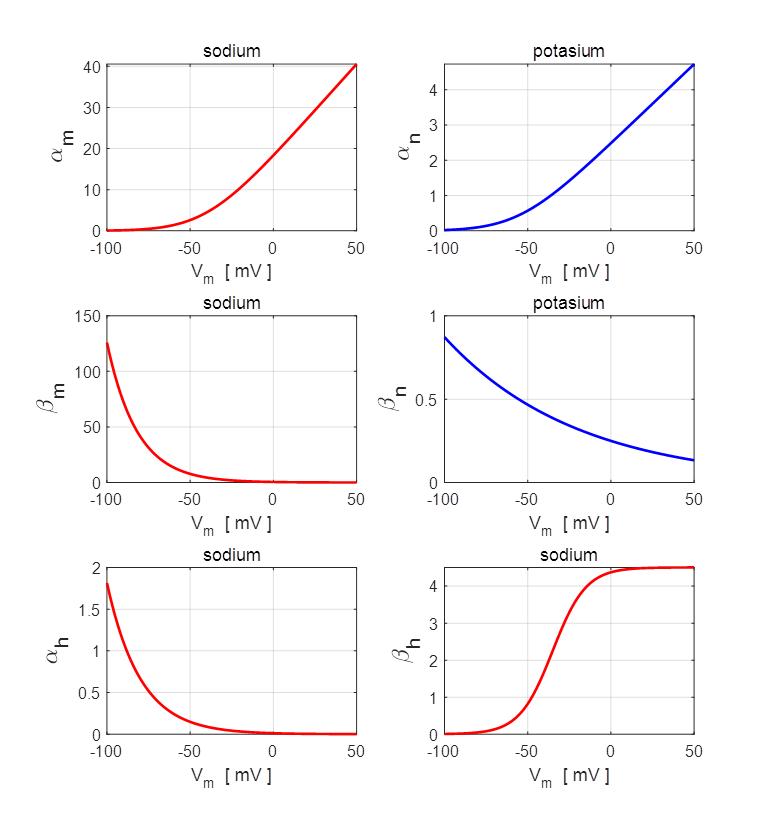
Fig. 4. Plots of the rate constants (T = 20 ^oC and V_rest = -65 mV). npIC.m

In order to getter a better understanding of the three gating variables ( x = m or n or h) given in equation 4, it is convenient to rewrite each of the equations in the form

(5A)

(5B)

(5C) asymptotic value of x

(5D) time constant

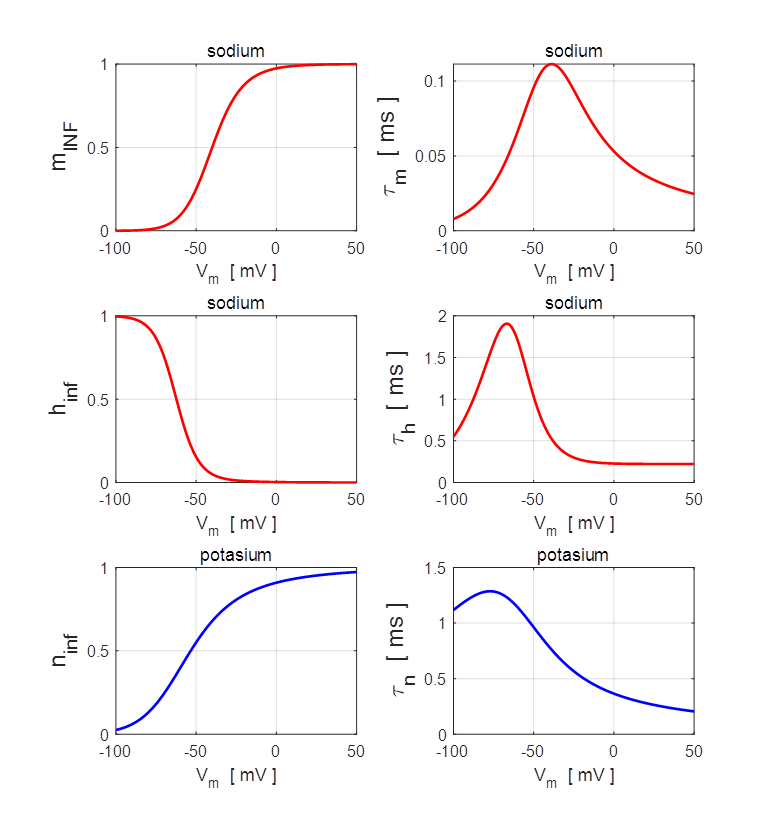
For a fixed voltage V_m, the variable x approaches the value with a time constant .

Fig. 5. The steady values of (m_¥, h_¥, n_¥) and their corresponding time constants (t_m, t_h, t_n ) as functions of the membrane potential. The variables m and n are activating gate variables (increase in values as V_m increases). h is an inactivating gate variable (h decrease as V_m increases). The activation of the sodium ion channel (m) for the influx Na⁺ is much quicker than the response of the out flux of K⁺ ions (n) or the deactivation of the sodium ion channels (h) since .

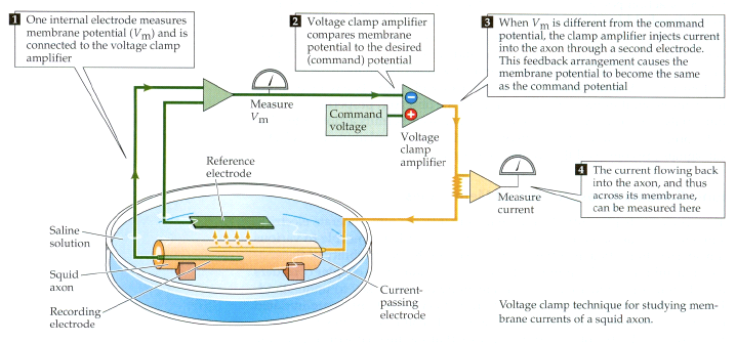
T = 20 ^oC and V_rest = -65 mV npIC.m

VOLTAGE-CLAMP SIMULATIONS

In many of the experiments performed by Hodgkin and Huxley, they held the membrane at a fixed voltage by inserting an electrode into the axon of a squid.

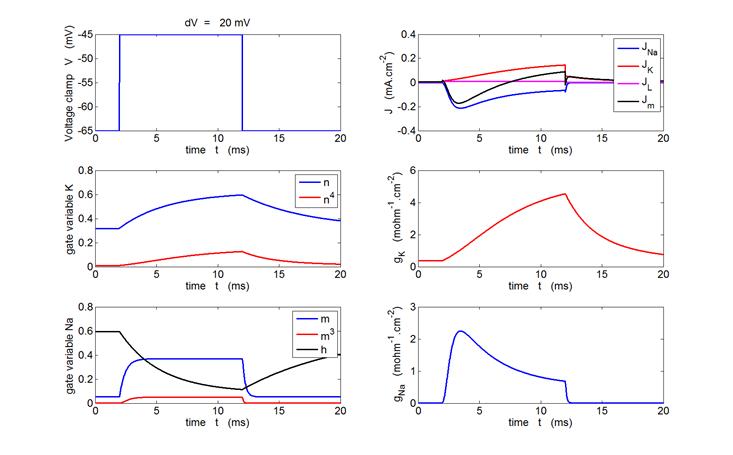
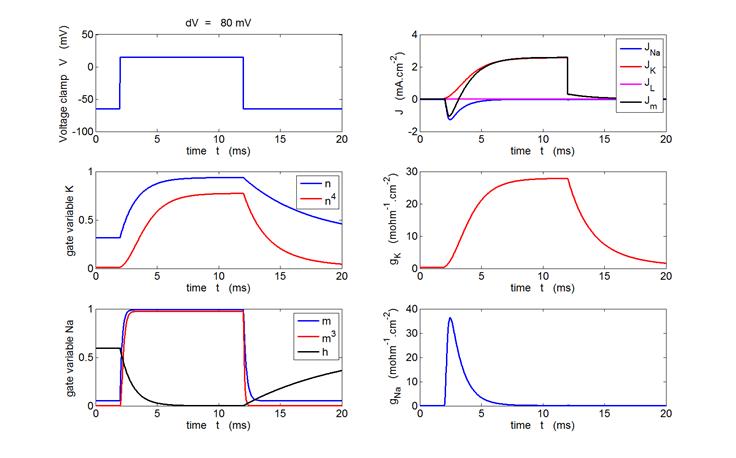
Fig. 6. Voltage-clamp of a squid axon.

The Matlab m-script bp_neuron_02.m can be used to calculate and display the voltage-clamp, the current densities (J_m, J_L, J_K and J_Na), the gate variables (m, m³, h and n, n⁴) and the conductances (g_Na, g_K). Sample graphical outputs are shown in figure 7 for voltage clamps of +20 mV and +80 mV.

Outline the m-script bp_neuron_02.m structure

· Default resting potential V_r = -65 mV

· Voltage clamp is given as a long pulse

· Rate constants a and b are calculated using the functions alpha.m and beta.m

· As the time variable is incremented, the gates variables (n, m, h) then the conductances (g_Na and g_K) then the current densities (J_NA, J_Na and J_M) are calculated for each time step. The gate variables are calculated from equation (12) by using the finite difference method to approximate the first derivative:

nt(c+1) = nt(c) + dt * (An(c) *(1-nt(c)) - Bn(c) * nt(c));

mt(c+1) = mt(c) + dt * (Am(c) *(1-mt(c)) - Bm(c) * mt(c));

ht(c+1) = ht(c) + dt * (Ah(c) *(1-ht(c)) - Bh(c) * ht(c));

Fig. 7. Variation in the gate variables, conductances and current densities for a voltage-clamp applied to the axon. The depolarization produced by the clamp causes a transient increase in Na⁺ into the cell. The rise in the K⁺ current from the cell occurs more slowly and is maintained as long as the membrane is depolarized. The rate of rise of the Na+ and K+ currents increases with increasing size of the voltage clamp and the peak values of Na⁺ and K⁺ currents are significantly increased as the clamp voltage is increased, the peak values are over 100 times the magnitudes in the resting membrane. bp_neuron_02.m