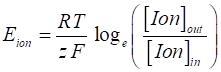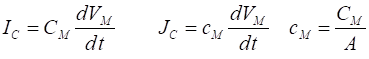|
COMPUTATIONAL NEUROSCIENCE NEURON MEMBRANE
CURRENTS REVERSAL (NERNST
– EQUILIBRIUM) POTENTIALS Ian Cooper Any
comments, suggestions or corrections, please email me at matlabvisualphysics@gmail.com |
|
MATLAB |
|
INTRODUCTION Electrical activity in neurones is sustained
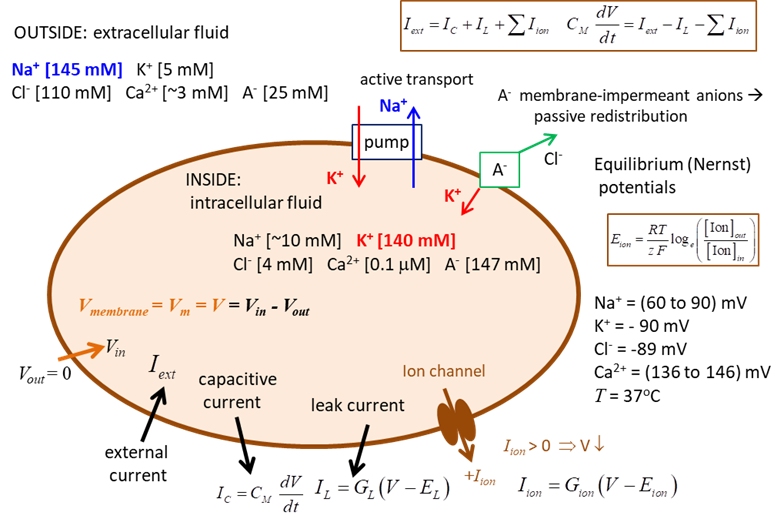
and propagated by ion currents through neurone membranes as shown in figure 1.
Most of these transmembrane currents involve four
ionic species: sodium Na+, potassium K+, calcium Ca2+
and chloride (Cl-). The concentrations
of these ions are different on the inside and outside of a cell. This creates
the electrochemical gradients which are the major driving forces of neural activity.
The extracellular
medium has high concentration of Na+ and Cl-
and a relatively high concentration of Ca2+. The intracellular medium has high concentration of K+
and negatively charged large molecules A-. The cell membrane has
large protein molecules forming ion channels through
which ions (but not A-) can flow according to their
electrochemical gradients. The concentration asymmetry is maintained
through ·
Passive redistribution: The impermeable anions A-
attract more K+ into the cell and repel more Cl-
out of the cell. ·
Active transport: Ions are pumped in and out of
the cell by ionic pumps. For example, the Na+/K+ pump,
which pumps out three Na+ ions for every two K+ ions
pumped.
Fig. 1. Electrophysiology of a neurone. Nernst or Equilibrium Potential There are two forces that drive each ion
species through the membrane channel. (1)
Concentration gradient: ions diffuse down the
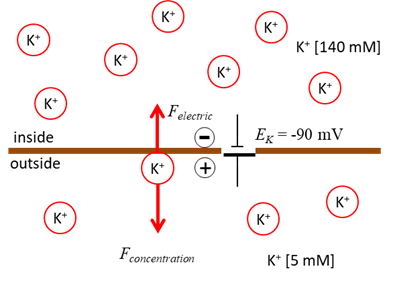
concentration gradient. For example, the K+ ions diffuse out of
the cell because K+ concentration inside is
higher than outside. (2)
Electric potential gradient: as ions diffuse across the
membrane a charge imbalance occurs producing a potential difference between
the inside and outside of the cell. For the K+ ions exiting the
cell, they carry positive charge with them and leave a net negative charge
inside the cell (consisting mostly of impermeable anions A-),
thereby producing the outward K+ current. The positive and negative charges accumulate
on the opposite sides of the membrane surface creating an electric potential
gradient across the membrane. This potential difference is called the transmembrane potential or membrane voltage (1) where the extracellular potential is
the reference potential such that This potential slows down the diffusion of K+,
since K+ ions are attracted to the negatively charged interior and
repelled from the positively charged exterior of the membrane. At some point an equilibrium is achieved. When the concentration
gradient and the electric potential gradient exert equal and opposite forces
on the ions, the net cross-membrane current is zero. The value of such an equilibrium potential depends on the ionic species and
it is given by the Nernst equation (2) where [Ion]in and [Ion]out are concentrations
of the ions inside and outside the cell respectively, R is the universal gas constant (R = 8.3155 J.mol-1.K-1),
T is temperature in degrees Kelvin, F is Faraday’s (F = (96 485 C.mol-1), z is the valence of the ion (z = 1 for Na+ and K+,
z = -1 for Cl-, and z = 2 for Ca2+). Eion is also called the reversal potential.
Fig. 2. Diffusion of K+ ions
down the concentration creates an increasing electric force directed in the
direction opposite to the force due to the concentration difference until the
diffusion and electrical forces balance each other. Membrane Currents We can model the movement of ions
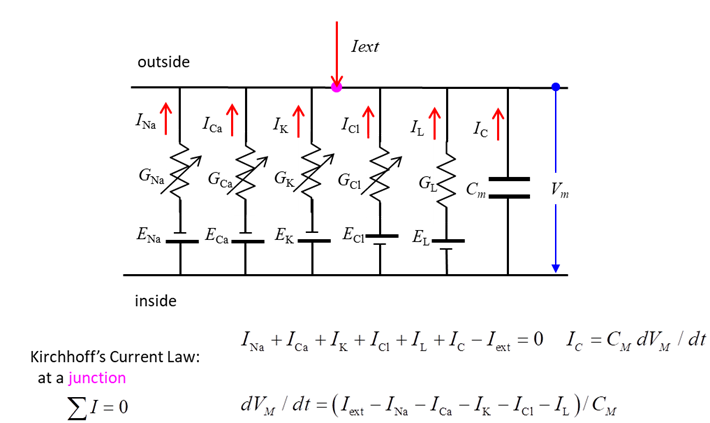
across the membrane as an electric circuit as shown in figure 3.
Fig. 3. Equivalent
circuit representation of a nerve cell membrane. In the neuroscience literature,
there is often some confusion and inconsistencies in the use of scientific
language and the units used for physical quantities. For example, the terms
conductance and conductance per unit area are often not distinguished and g maybe the conductance or
conductance per unit area with units S or S.cm-2. In Izhikevich’s book, he gives the current in In the Scripts to model the
dynamic behaviour of neurones, S.I. units are used
for all input parameters and calculations. However, results may be expressed
in non S.I. units, for example, mV for voltage. The current through a resistive
element can be expressed by the equation
(3)
I current [ampere A] V potential difference [volts V] R resistance [ohm G conductance [Siemens S 1 S This equation can also can also be
expressed in expressed in terms of the current density
(4)
A area [m] J current
density [A.m-2] g specific conductance [S.m-2] The major ion currents shown in
figure 2, can be expressed as
(5) X
ion (e.g.
Na+ K+ leakage) VM membrane
potential (voltage) [volt V] EX
equilibrium (Nernst) potential
[V] When the conductance is constant,
the current is said to be ohmic.
In general, ionic currents in neurones are not ohmic, since the conductance
may depend upon time, membrane potential, and
pharmacological agents (e.g. neurotransmitters). It is the time-dependent
variation of conductances that allow a neurone to generate an action
potential (spike). The membrane acts like a capacitor
– an insulator (membrane) surrounded by the extracellular and
intracellular fluids (conductive plates). When the membrane potential
changes, a current is generated to charge or discharge the capacitor. The
capacitor current is given by the time derivative of the voltage
(6) CM
capacitance [F] cM specific
capacitance [F.m-2] The equivalent circuit to
represent the electrical properties of membranes is shown in figure 3.
According to Kirchhoff’s Current Law, the sum of the currents entering
and leaving a junction must add to zero. Hence across the membrane
(7)
Therefore, we can write an “equation
of motion” to describe the dynamical system of a neurone as
(8) Note:
The membrane potential is
typically bounded by the equilibrium potentials
One example of the application of
equation (8) is the Hodgkin-Huxley
Model. For different models of a neurone, equation
(8) can be solved using the Matlab ordinary differential equation solver ode45. |