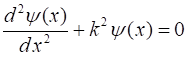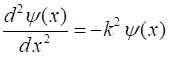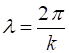DOING PHYSICS WITH MATLAB

NORMAL TRANSVERSE MODES OF A VIBRATING ROD

EIGENVALUES and EIGENFUNCTIONS

Any comments, corrections or suggestions, please email Ian Cooper at

matlabvisualphysics@gmail.com

MATLAB SCRIPTS

wmRodm.m

https://github.com/D-Arora/Doing-Physics-With-Matlab/blob/master/mpScripts/wmRod.m

wmRod.mlx (live editor version)

https://github.com/D-Arora/Doing-Physics-With-Matlab/blob/master/mpScripts/wmRod.mlx

The eigenvalues and eigenfunctions for the transverse normal modes of a vibrating rod are found using the Matlab function eig.

For a more in-depth treatment visit

HELMHOLTZ EQUATION - EIGENVALUE PROBLEM - STANDING WAVE ANIMATIONS

The spatial wavefunction describing the transverse normal modes of a vibrating of a rod can be found from the Helmholtz equation

(1) or

where the wavefunction describes the transverse displacement of the rod and k is the wavenumber. The wavelength for a normal mode of vibration of the rod is

(2)

This is simply an eigenvalue problem, where is the eigenfunction and E is the corresponding eigenvalue.

The second derivative of the wavefunction can be approximated by the finite difference approximation

(3)

The X domain is divided into N+2 evenly spaced grid points where . The ends of the rod are and where L is the length of the rod. The normal modes of vibration are determined by the solutions of equation 1 that satisfy the imposed boundary conditions

Fixed / Fixed ends (Node/Node)

Fixed / Free ends (Node/Antinode)

Free / Free ends (Antinode/Antinode)

For the interior grid points, equation 1 can be expressed in matrix form

(4)

where is a matrix of dimensions and is a column vector with elements . The elements A(1,1) and A(N,N) are determined by the boundary conditions. The eigenvalue E is

(5)

The eigenvalues and eigenvectors are found using the Matlab function eig.

% Eigenvalue Matrix A: eigenfunctions (eignFN) / eigenvalues (eignV)

off = ones(N-1,1);

A = - diag(off,-1) + 2*eye(N) - diag(off,1) ;

if BC == 2; A(N,N) = 1; end % fixed free

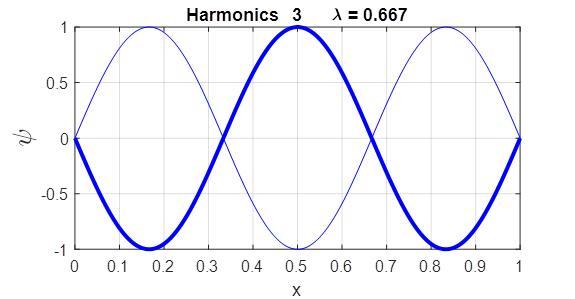
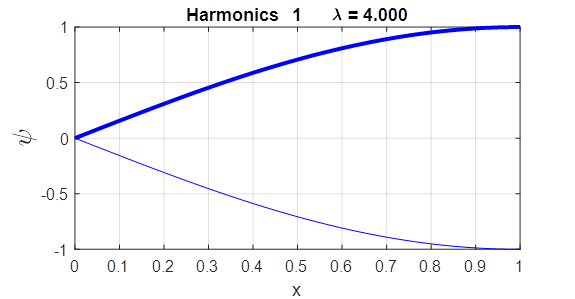
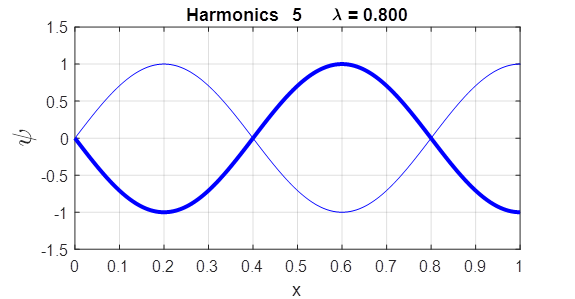
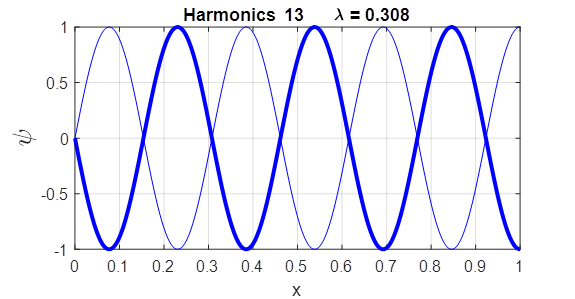
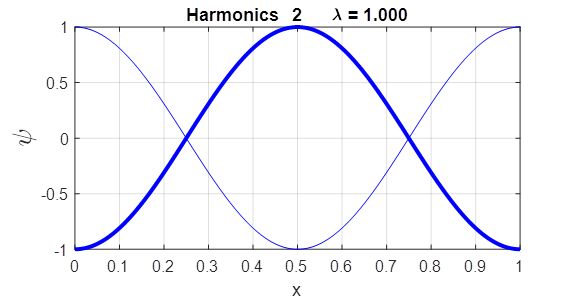
if BC == 3; A(1,1) = 1; A(N,N) = 1; end % free free

[eignFN, eignV] = eig(A);

Each column of the first matrix eignFN is the eigenvector (eigenfunction) and the diagonal elements of the second matrix eignV are the eigenvalues.

Using the Live editor version of the Script wmRod.mlx, one can change the boundary conditions and mode number and view a plot of the wavefunction immediately. The title of the plot shows the harmonic displayed and the wavelength.

EXAMPLES

Rod fixed at both ends

Rod fixed / free ends

Rod free / free ends