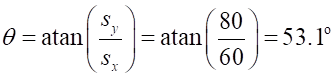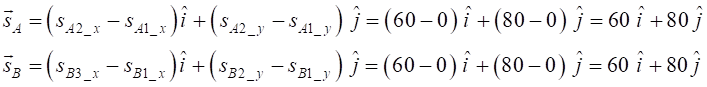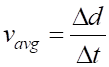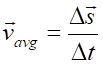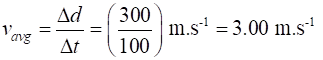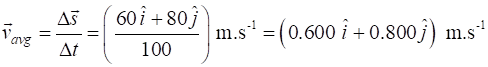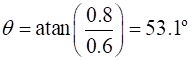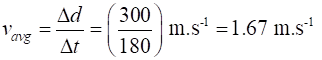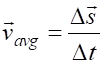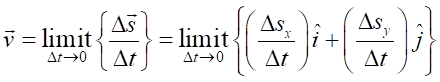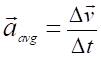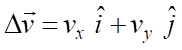|
KINEMATICS DESCRIBING MOTION Ian Cooper email matlabvisualphysics@gmail.com The language used to describe motion is called kinematics.
Surprisingly, very few words are needed to fully the describe the motion of a
System. Warning:
words used in a scientific sense often have a different interpretation to the
use of those words in everyday speech. The language needed to fully describe motion is outlined in Table 1.
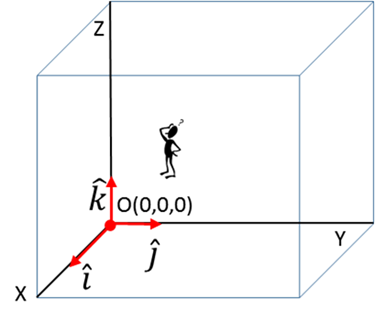
In analysing the motion of an object or collection of objects,
the first step you must take is to define your frame of
reference. Frame
of reference Observer Origin O(0,0, 0) reference
point Cartesian
coordinate axes (X, Y, Z) Unit
vectors Specify
the units
Table1. Kinematics: terminology for the
complete description of the motion of a System in a plane. POSITION DISTANCE DISPLACEMENT Consider
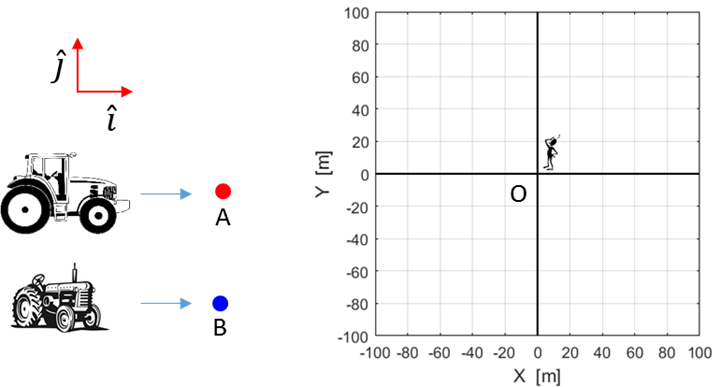
two tractors moving about a paddock. To study their motion, the frame of
reference is taken as a XY Cartesian Coordinate System
with the Origin located at the centre of the paddock. The stationary observer
is located at the centre of the paddock and the metre is the unit for a distance
measurement. The positions of the tractors are given by their X and Y
coordinates. Each tractor is represented by a dot and the tractors are identify using the letters A and B.
Fig.
1. Frame of reference used to
analyse the motion of the two tractors in a plane. Both
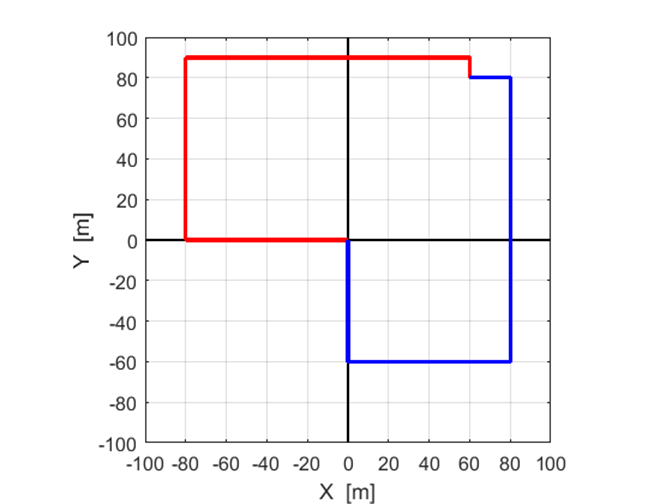
tractors move from their initial position at the Origin O(0,
0) to their final position at (60, 80) as shown in figure (2). Tractor A
follows the red
path and tractor B follows the blue path. Event 1 corresponds to
the initial instance of the tractor motion and Events 2 and 3 are the
instances when the tractors each their final position.
Fig.
2. RED path of tractor A and BLUE
path of tractor B. Both tractors start at the Origin O(0, 0) and finish at the point (60 m, 80m).
Event
1 Position
of tractors System
A System
B N.B. The first subscript is used to identify the System and
the second the time of the Event. Remember we are using a model – in
our model it is possible for both tractors to occupy the same position at the
same time. Event
2 System
A Event
3 System
B Distance travelled Using
figure (2), it is simple matter to calculate the distance System
A System
B Displacement
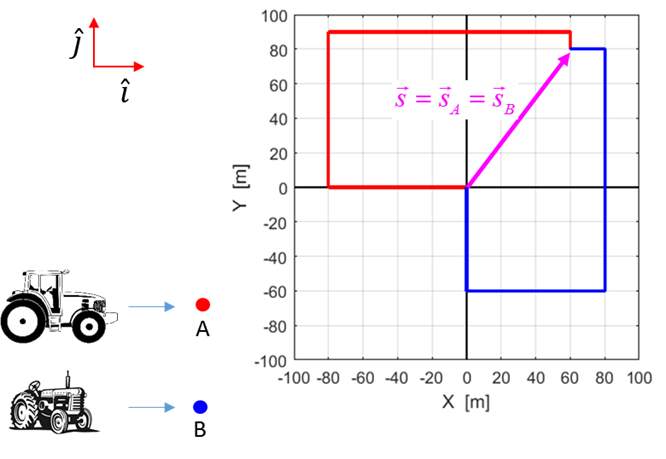
Position Vector The change
in position of the tractors is called the displacement. The displacement
only depends upon the initial position (Event 1) and final position (Events 2
and 3) of the System and not with any details of what paths were taken during
the time interval between the two Events. The
displacement is represented by the position vector and is drawn as a straight
arrow pointing from the initial to the final position as shown in figure (3).
The
tractors start at the same position and finish at the same position,
therefore, they must have the same displacement, even though they have
travelled different distance in different time intervals.
Fig.
3. The displacement of the
tractors shown as a position vector. From figure
(3), it is obvious the values for the component of the position vector are The
magnitude of the displacement is The
direction of the displacement is given by the angle N.B. The distance travelled (scalar) and the displacement
(vector) are very different physical quantities. The
displacement gives the change in position as a vector, hence we can write the
displacements for System A and System B as
Multiple subscripts look confusing, but, convince yourself
that you can interpret the meaning of all the symbols. Once you get
“your head around it”, using multiple subscript means that you
can convey a lot of information very precisely. AVERAGE SPEED AVERAGE VELOCITY “Time
is a measure of movement”
Aristotle (384 – 322 BC) The
time interval between Event 1 and Event 2 be given by
In
this time interval, the change in position is given by distance travelled
displacement
The
definition of the average speed is (1) The
definition of average
velocity is (2) Warning: the magnitude of the average velocity The average speed and average velocity are
different physical quantities. From the
information for the motion of the two trajectories of tractors A and B shown
in figure (3), we can calculate the average speed and average velocities of
each System. System
A (tractor A) red path Time interval between Event 1
and Event 2 Distance travelled Displacement
Using
equations (1) and (2) Average speed Average velocity vector / same direction as the displacement
Using the components of the average velocity magnitude direction
The average speed and average velocity are
different physical quantities. System
B (tractor B) blue path Time interval between Event 1
and Event 3 Distance travelled Displacement
Using
equations (1) and (2) Average speed Average velocity INSTANTANEOUS SPEED INSTANTANEOUS VELOCITY On most occasions, we want to know more than just averages, we want details about the dynamic motion of a particle
on an instant-by-instant basis. The
definition of average velocity is (2) If
we make the time interval This
limit is one way of defining the derivative of a function. The instantaneous
velocity is the time rate of
change of the displacement (3) In terms of vector components for the displacement and velocity
(4)
As the time interval approach zero When
you refer to the speed or velocity it means you are talking about the
instantaneous values. Therefore, on most occasions you can omit the word
instantaneous, but you can’t omit the term average
when talking about average
speed or average
velocity.
ACCELERATION An
acceleration
occurs when there is a change in velocity with time. ·
Object
speeds up ·
Object
slows down ·
Object
change’s its direction of motion The average
acceleration of an object is
defined in terms of the change in velocity and the interval for the change (6) The
instantaneous acceleration (acceleration)
is the time rate of change of the velocity, i.e., the derivative of the
velocity gives the acceleration (equation 7). (7) In terms of
vector components for the velocity and acceleration (4)
|