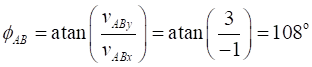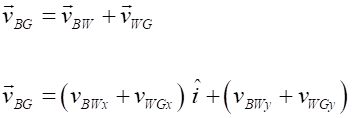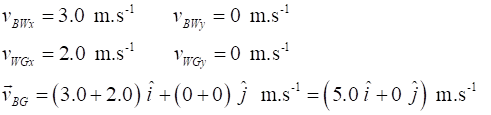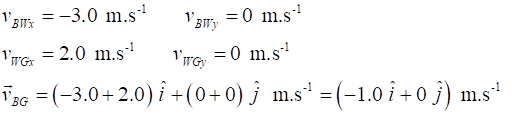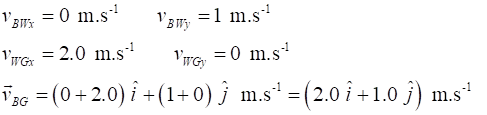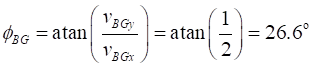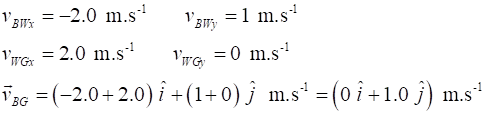|
RELATIVE MOTION
RELATIVE VELOCITY Ian Cooper email matlabvisualphysics@gmauil.com The velocity of an
object depends upon the motion of an observer. Therefore, velocity is a relative concept. Again, consider our two
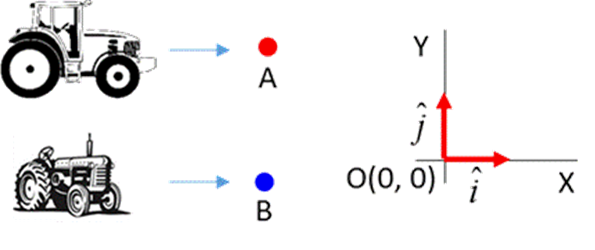
tractors represented as point particles and identified as System A and System
B as shown in figure (1). The two tractors start at the Origin O(0, 0) and then move away from the Origin with different
constant velocities. Fig.
1. The two tractors are
represented as point particles and identified as
System A
and System B.
Remember, the first step in any motion problem is to define a frame of
reference.
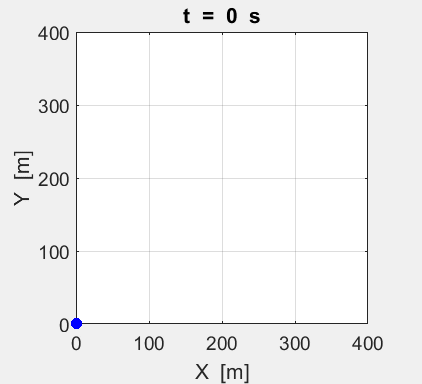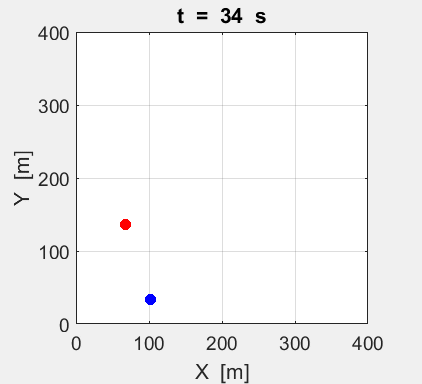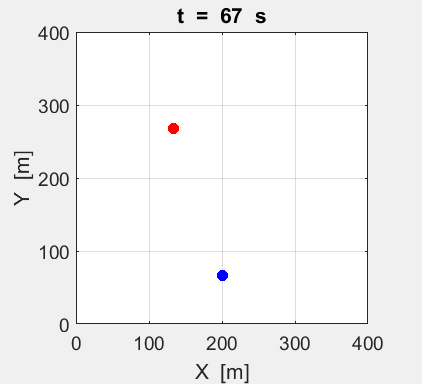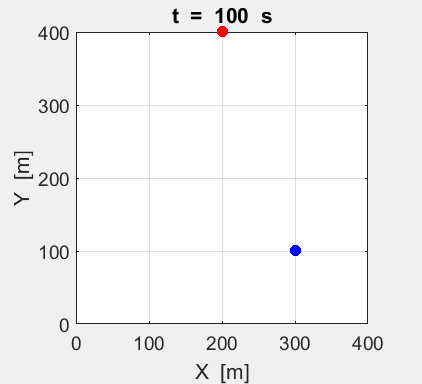
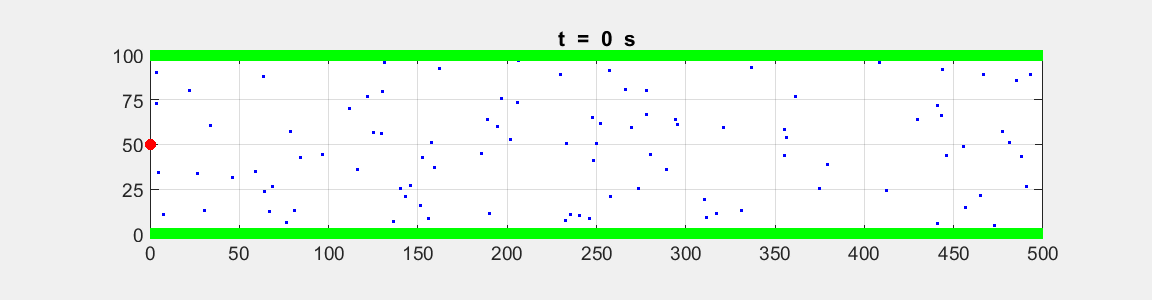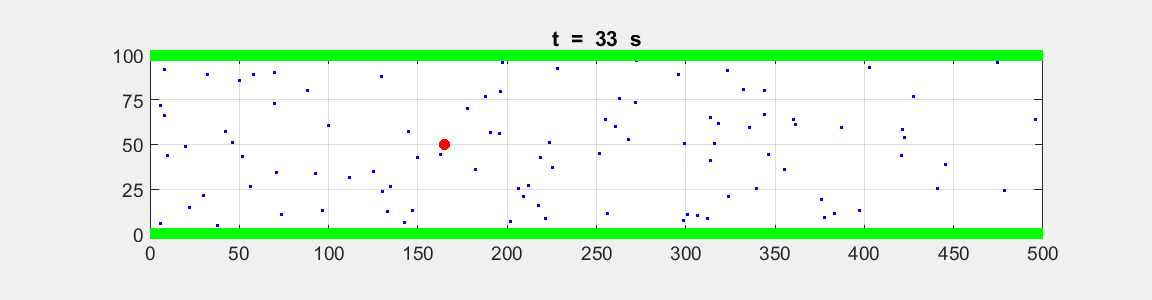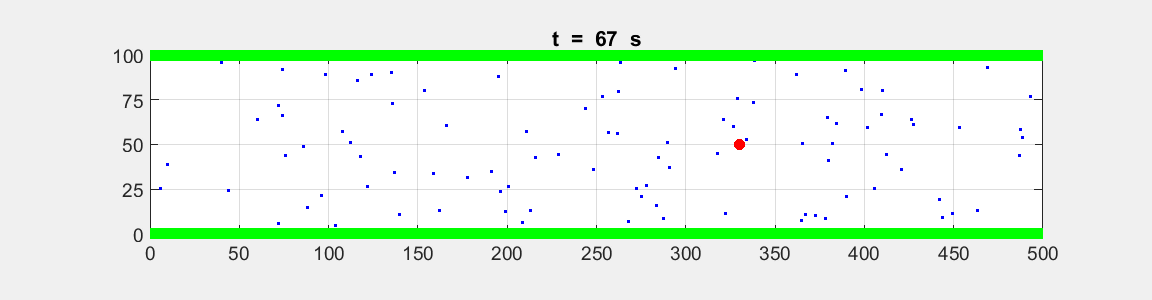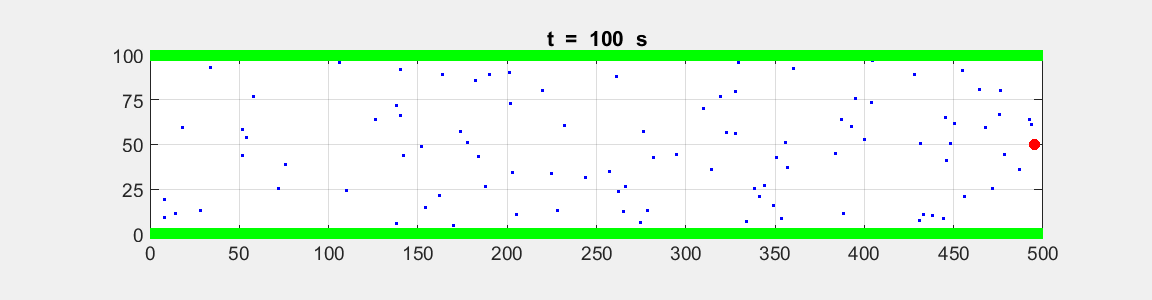
Fig. 2A. Animation of the motion of the
two tractors moving with constant velocities. The red dot shows the motion for
System A and the blue dot
for System B.
Event 1: position of the Systems at t = 0 s. Event 2: position of the Systems at t = 100 s.
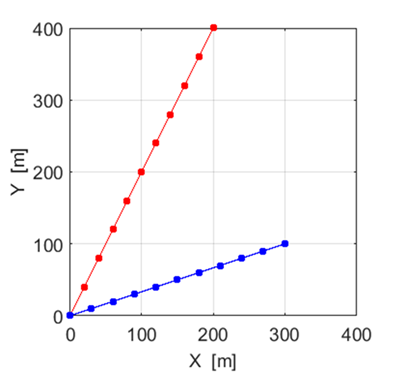
Fig.
2B. Path of the two
tractors with the position of System A and System B shown at 10 s intervals. Exercise 1 By
careful examination of the animation, answer the following questions (answers
at end of document): 1. For
Event 2 when t = 100 s, what are
the final displacements of the two Systems? For the displacement of each
System, give the numerical values for: the components, magnitudes and
directions. 2. What
is the velocity of each System?
(components, magnitudes, directions). 3.
Draw the magnitudes of the displacements
verses time graphs for Systems A and B (include appropriate scales). 4.
Draw the magnitudes of the
velocities verses time graphs for Systems A and B (include appropriate
scales). The description of the
motion from an observer stationary w.r.t. System B So
far we have considered the motion of our two Systems from the point of view
of a stationary observer. We will now consider an observer (Pat) in tractor B.
From Pat’s point of view, the System B is stationary at all times But what does Pat conclude about the motion of System A? To
answer this question, we need to find out the velocity of System A
w.r.t. System B
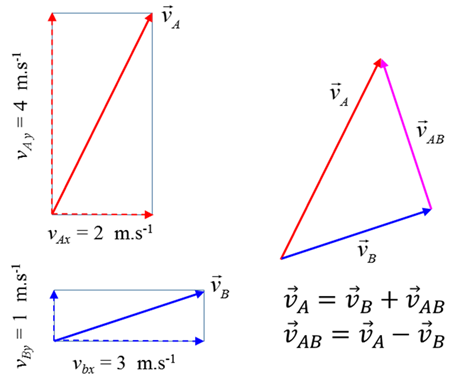
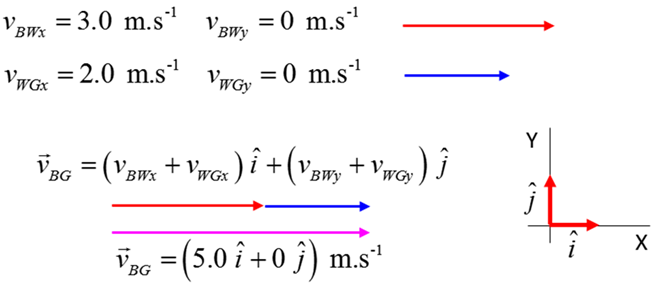
as given by the vector N.B. The first subscript identifies the System A and the second subscript identifies the observer B (reference point). The
relative velocity of A w.r.t. B is given by the vector equation The answers from Exercise 1 give the values for the velocities of the
two Systems
Therefore,
the relative velocity of System A w.r.t. System B is
magnitude
direction
N.B. The relative
velocity is found by the process of vector subtraction. View
the animation again and notice that w.r.t. System B, System A is moving away from B in
a positive Y direction and a negative X direction as given by the numerical
results. Figure 5 shows the
velocity vectors which describe the relative motion of System A
w.r.t. System B.
Fig.
5. Vector diagrams
illustrating the relative velocity of System A w.r.t System B.
The relative velocity is found by vector subtraction. In drawing a vector and its components, it is good technique
to draw a rectangle around the vector in a light colour. The vector is the diagonal
of the rectangle and the sides are the components. The vector components
replace the original vector and so in the diagram either the vector or its
components can be shown as dashed lines to reinforce the fact there is only
one vector. The vector diagrams can be drawn to scale to make measurements. The use of unit vectors simplifies the mathematics. Enough
though the concept of unit vectors is usually not used at the high school
level, it is a better approach for such problems than any alternative
methods. MOTION OF A BOAT
IN A RIVER
The
motion of the boat through the water depends upon the velocity of the boat
through the water and the velocity of the water itself. We
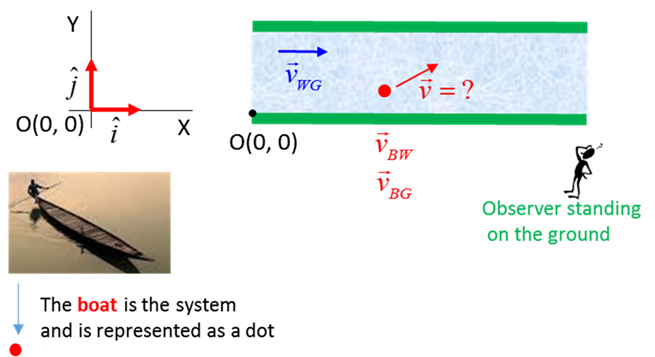
need to define a frame of reference to investigate the motion of the boat. We
will use an XY Cartesian coordinate System with
Origin O(0, 0) and a stationary observer standing on
the ground (G).
Fig.
6. Frame of reference for the
boat moving through the water in a river. Velocity is a relative
concept The
motion of the boat through the water depends upon the velocity of the boat
through the water and the velocity of the water itself. We
need to define a frame of reference to investigate the motion of our boat
through the water in a river as shown in figure (6). The
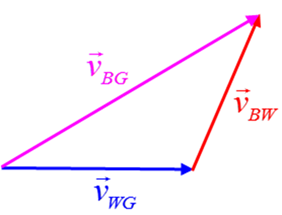
best way to specify the velocities is to use appropriate subscripts · velocity
of water w.r.t. ground
· velocity
of boat w.r.t. ground · velocity
of boat through water (velocity
of boat w.r.t. water)
The
velocity of the boat with respect to ground
(1)
Exercise 2 Carefully
view the animation shown in figure (EX2) to estimate numerical values for: 1. The
velocity of the water w.r.t. the ground 2. The
velocity of the boat w.r.t to the ground 3. The
velocity of the boat through the water (w.r.t water) 4. Draw
a set of vector diagrams (scaled) to represent each vector and the addition
of vectors to give the resultant. 5. Think
about what direction the boat must head to travel directly across the river.
Fig. EX2. Motion of a boat moving
downstream in the river. Exercise 3 1. Carefully
view the animation shown in figure (EX3) to estimate numerical values for: 2. The
velocity of the water w.r.t. the ground 3. The
velocity of the boat w.r.t to the ground 4. The
velocity of the boat through the water (w.r.t water) 5. Draw
a set of vector diagrams (scaled) to represent each vector and the addition
of vectors to give the resultant.
Fig. EX3. Motion of a boat moving upstream
in the river. Exercise 4 Carefully
view the animation shown in figure (EX4) to estimate numerical values for: 1. The
velocity of the water w.r.t. the ground 2. The
velocity of the boat w.r.t to the ground 3. The
velocity of the boat through the water (w.r.t water) 4. Draw
a set of vector diagrams (scaled) to represent each vector and the addition
of vectors to give the resultant. 5. In
what direction is the boat heading?
Fig. EX4. Motion of a boat across the
river. Exercise 5 Carefully
view the animation shown in figure (EX5) to estimate numerical values for: 1. The
velocity of the water w.r.t. the ground 2. The
velocity of the boat w.r.t to the ground 3. The
velocity of the boat through the water (w.r.t water) 4. Draw
a set of vector diagrams (scaled) to represent each vector and the addition
of vectors to give the resultant. 5. In
what direction is the boat heading?
Fig. EX5. Motion of a boat moving directly
across the river. Exercise 1 Answers
Event 2: System A System B
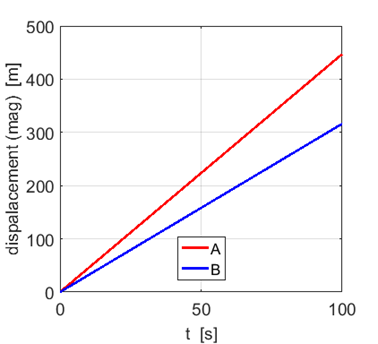
Exercise 1.3 Magnitude
of the displacements for the two Systems A and B. The slope of the tangent to the displacement
/ time curve gives the magnitude of the velocity. Since the slopes of the two
lines are constant, the velocities of Systems A and B are constant. The numerical
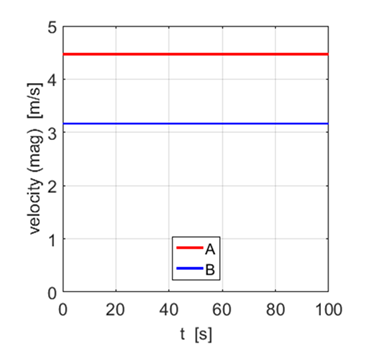
value of the slope of the line is equal to the magnitude of the velocity. Exercise 1.4 The
magnitudes of the velocities for Systems A and B.
Exercise 2 Answers
For
our stationary observer standing on the ground, the boat moves straight down
the river with a velocity of 5.0 m.s-1 in the
same direction as the flow of water.
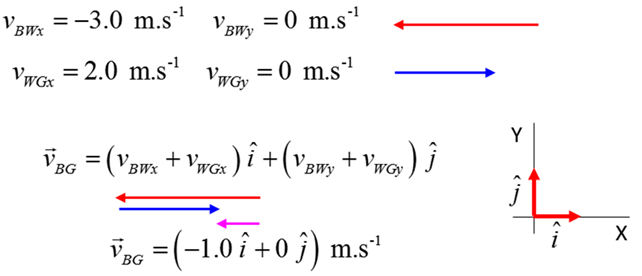
Exercise 3 Answers
For
our stationary observer standing on the ground, the boat moves straight up
the river with a velocity of 1.0 m.s-1 in the opposite direction
to the flow of water.
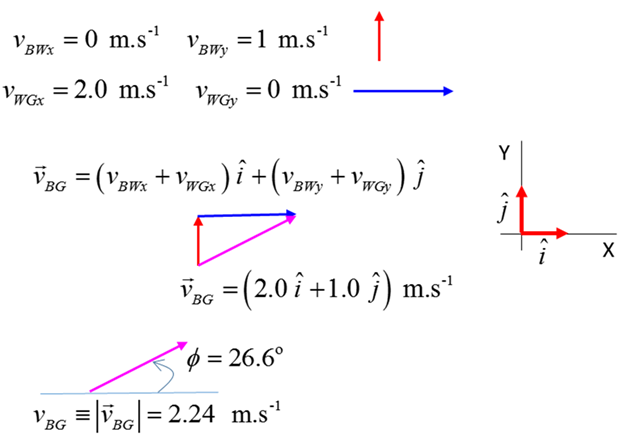
Exercise 4 Answers
magnitude
direction For
our stationary observer standing on the ground, the boat moves across the
river with a velocity of 2.24 m.s-1
at an angle of 26.6o w.r.t. the bank of
the river.
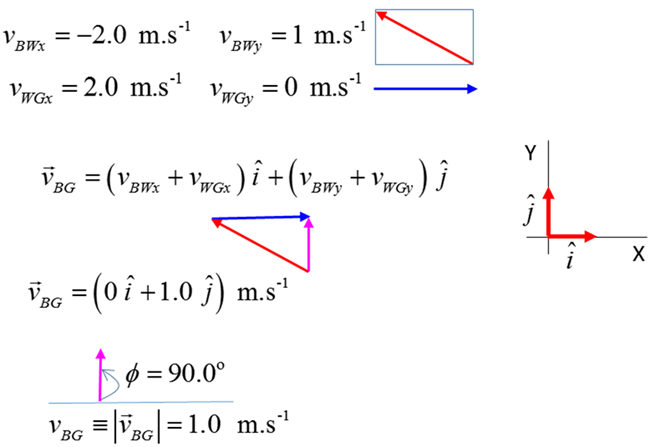
Exercise 5 Answers
magnitude
direction For
our stationary observer standing on the ground, the boat moves directly
across the river with a velocity of 1.0 m.s-1 .
QUESTIONS and
PROBLEMS with ANSWERS Identify Û
Setup Û
Execute Û
Evaluate Your major goal should
be to improve your understanding of our physical world through Physics by
doing lots of problems. This is not achieved by just picking a formula and
“throwing” in the numbers to get a quick answer. Getting the
right or wrong answer to a question is not important. The important things
are your improvement in creativity; thinking ability; understanding; problem
solving skills and techniques; and knowledge. Step
1. “Close your
eyes” and try to visualize the physical situation and make predictions
about the motion. The greatest physicists such as Einstein, Feynman and Fermi
did not just grab a formula – they were creative thinkers who could
visualize the world around them. For example, you have a question on an aircraft, visualize the plane in motion and how it would
be effected by the air currents and think about approximation and/or
simplifications that need to be made. Step
2. Think about what category the problem
relates to and what approach should I use. Step
3. Create a scientific annotated
diagram which may include: frame of reference; the Systems of interest; a dot
(point particle) representing a System; list the given and implied values
with appropriate use of symbols, subscripts and units; list the unknown
physical quantities; fact, laws and principles. Step
4. Answers the question. Step
5. Evaluate your answer. How-to approach the relative motion problems · Visualize the
relative motion of the objects. · Define the
frame of reference: XY Cartesian axes; Origin; unit
vectors; observers (reference points); units. · Identify the Systems
of interest and key features. A System is represented by a dot. · Identify all
vector quantities: magnitudes; directions; X and Y components; specify a
vector in terms of the unit vectors; use appropriate symbols and subscripts. · Use the methods
of vector addition and subtraction using components and/or scaled vector
diagrams. You need to know about the geometrical properties of a right-angle
triangle. · Check you
answer: sensible; significant
figures; units; does your answers agree with your predictions from
visualising the physical situation? · In a
calculation, never mix numbers and units. Units should always be placed on
the far right of the expression as shown in the answers. |