VISUAL PHYSICS ONLINE

RELATIVE MOTION: POSITION

Ian Cooper

email matlabvisualphysics@gmail.com

In analysing the motion of an object or collection of objects, the first step you must take is to define your frame of reference and identify the System.

Observer

Origin O(0,0, 0) reference point

Cartesian coordinate axes (X, Y, Z)

Unit vectors

Specify the units

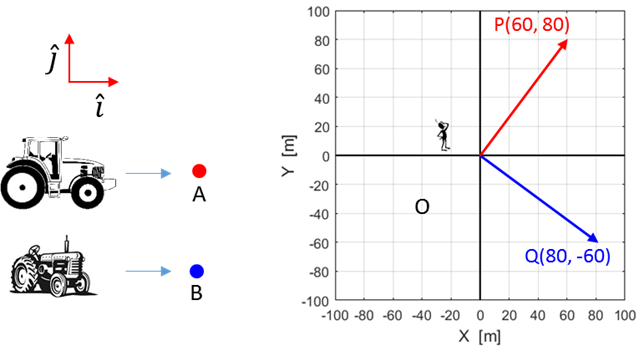
The position of an object (System represented by a point particle) can be specified by its position vector corresponding to the displacement of the system from the Origin O(0, 0).

Again, we will consider our two tractors as systems A and B. The location of the two Systems and their position vectors with respect to the Origin O(0,) are shown in figure (1). System A is located at the point P(60, 80) and System B is located at the point Q(80, -60). The position vectors are

System A

System B

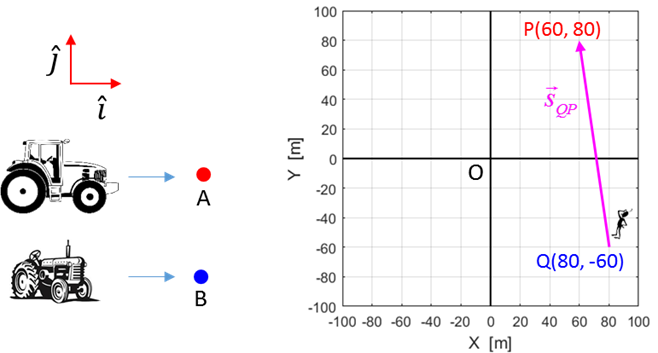
Fig. 1. The position vectors (displacements) of the two systems with respect to the Origin O(0, 0).

But what is the location of the tractor A for an observer in tractor B?

From the diagram, the point P is 20 m in the negative +X direction and 140 m in the +Y direction with respect to the point Q. Also, we can answer this question in terms of the relative position of the two points using vector quantities. The relative position of point P w.r.t to the point Q is given by the displacement as shown in figure (2). The first subscript P is the point of interest and the second subscript Q is the reference point.

Fig. 2. The relative position of the point P w.r.t. the point Q is given by the vector .

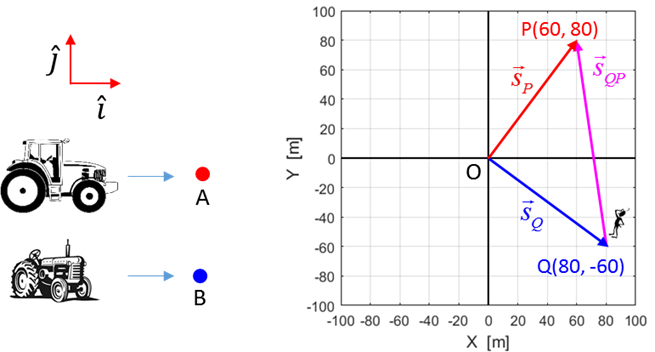
Figure 3 shows the displacement vector for the point P, the displacement vector for the point Q and the relative position vector for the position of P w.r.t. Q.

Fig. 3. The relative position of the point P w.r.t. the point Q is given by the vector . The displacements and are for the points P and Q w.r.t. the Origin respectively.

From figure (3) using the principle of vector addition it is obvious that

Therefore, the relative position of the point P w.r.t. Q is given by the vector

subtraction of vectors

The relative position in terms of components is

System A

System B

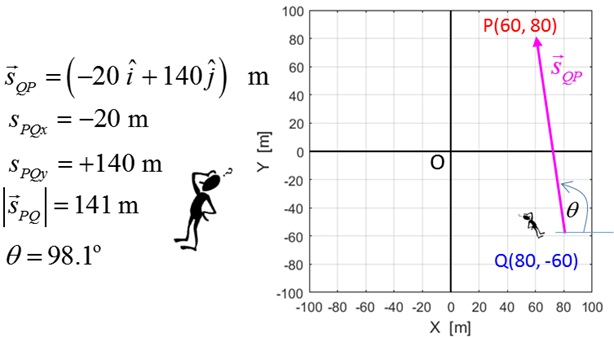
The magnitude of a vector is given by

positive scalar quantity

The direction of the vector is given by

measure w.r.t. +X axis

The relative position of point P w.r.t. the point Q is

w.r.t X axis

Fig. 4. Displacement is a relative concept. The relative position of the point P w.r.t the point Q is given by the displacement .