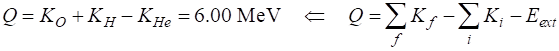|
SPECIAL RELATIVITY and NUCLEAR REACTIONS NUCLEAR TRANSFORMATIONS |
|
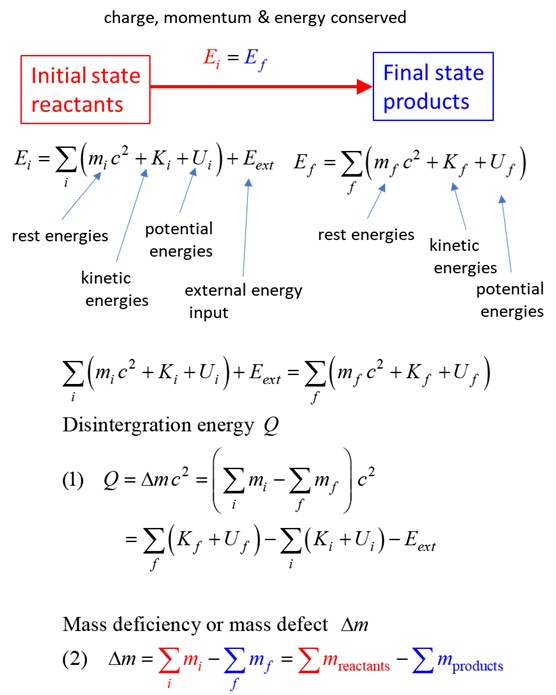
SUMMARY Total energy total
energy = rest energy + kinetic energy + potential energy
Law of
conservation mass-energy isolated
system E =
constant
The
energy released in nuclear reactions can be predicted form the theory of
special relativity and the predictions agree extremely well with measured
values. |
|
Energy / Mass units, values and conversion factors amu (atomic mass unit) = 1 u = 1.66054´10-27 kg 1 eV = 1.602´10-19 J 1 MeV = 106 eV A mass of 1 u
(1 amu) has an energy equivalent of: E = (1.66054´10-27) (2.99792´108)2 J = 1.49242´10-10 J E = 931.494
MeV 1 u º 931.494 MeV/c2 Proton mass mp = 1.67262´10-27 kg = 1.0072765 u = 938.3 MeV/c2
Neutron mass mn = 1.67493´10-27 kg = 1.0086649 u = 939.6 MeV/c2 Electron mass me = 9.1093897´10-31 kg = 0.0005485799 u = 0.511
MeV/c2 NUCLEAR TRANSFORMATIONS
Example 1 12C6 and 13C6 binding energy of the last neutron We can calculate the energy required to remove a single neutron from the nucleus of the isotopes carbon-12 and carbon-13
Initial state (reactants)
12C6
m(11C6) = 11.008142131544027 u m(1n0) = 1.008664915821551 u Mass: Reactants
11.996709 u Mass: Products
11.008142 u
1.008665 u
Mass defect dM
= -0.020099 u Disintegration value Q Q = -18.721659 MeV
Initial state (reactants)
13C6
m(13C6) = 13.000063355614028u m(1n0) = 1.008664915821551 u Mass:
Reactants
13.000063 u Mass:
Products
11.996709 u
1.008665 u Mass
defect dM
= -0.005310 u Disintegration
value Q Q = -4.946309
MeV The external work required to remove a neutron from carbon-12 is 18.7 MeV, whereas it required only 4.9 MeV to remove the neutron from carbon-13. Hence, it is much more difficult to remove a neutron from carbon-12 compared with carbon-13. Example 2 Will a reaction “go”? The isotope
carbon-13 is bombarded by 2.5 MeV protons to produce nitrogen-13 and a neutron. Can
the reaction happen?
Initial state (reactants)
13C6
+ 1H1 Mass: Reactants 13.000063 u
1.007276 u
Mass: Products 13.001899 u
1.008665 u
Mass defect dM
= -0.003224 u Disintegration value
Q Q = -3.002818
MeV The reaction is endothermic and requires 3
MeV to make the reaction go. Hence, the bombarding protons do not have enough
energy for the reaction to occur. The incident proton must have a kinetic
energy slightly greater than 3 MeV. Example 3 Oxygen can be produced by bombarding nitrogen with alpha particles
Initial state (reactants)
4He2
+ 14N7 Mass: Reactants 4.001506 u
13.999234 u
Mass: Products 16.994743 u
1.007276 u
Mass defect dM
= -0.001280 u Disintegration value Q Q = -1.191875
MeV Since
Q
< 0, this reaction does
not occur spontaneously. Ernest Rutherford used alpha
particles to bombard nitrogen target nuclei to produce oxygen and protons. If
the incident alpha particles had kinetic energy equal to 7.70 MeV, calculate
the Q-value
and the maximum kinetic energy of the protons and oxygen nuclei. Initial
state (reactants)
14N7
+ 4He2
mN = 13.999233945064699 u mHe = 4.001506094311343 u
mO = 16.994743117225369 u mH = 1.007276452320671 u
(nuclei masses quoted, not atomic
masses) Mass deficiency Disintegration energy The energy of 6.51 MeV is shared between the oxygen and hydrogen nuclei. RADIOACTIVITY AND
THE TRANSMUTATION OF THE ELEMENTS
Experimental work around the turn of
the 20th Century by Henri Becquerel (1852 - 1908), Ernest Rutherford (1871 -
1937), Marie Curie (1867 – 1934) and Pierre Curie (1859 – 1906)
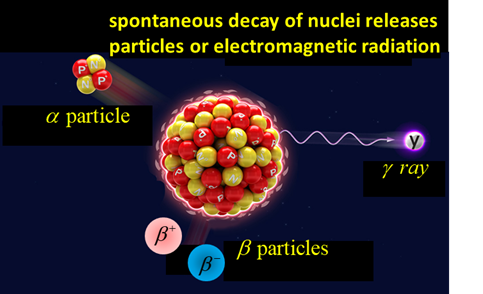
and others indicated that three kinds of natural radiations: alpha particles a, beta particles b and gamma rays g were emitted from a nucleus of an unstable atom. These radiations were emitted
naturally from certain elements such as uranium, polonium, radium, and
actinium. Further, it was found that the emission of natural radiations by
one element usually led to the production of a different element. For instance, radium was produced
because of the radioactive decay of uranium. This change of a parent nucleus into a different daughter nucleus is called a nuclear transmutation. One element effectively changes into
another element. When transmutation occurs, the sum
of the atomic numbers on the left-hand side of the nuclear equation equals
the sum of the atomic numbers on the right-hand side. Likewise, the sum of the mass numbers
on the left-hand side of the nuclear equation equals the sum of the mass
numbers on the right-hand side.
Gamma decay beta
particles: electron |
|
neutrino |
|
Example 1 Image that you are given the task of
producing a 10 minute video clip for YouTube as an introductory lesson on
special relativity. Make a list of the concepts that you would introduce.
What images and animations would you include? Watch Vdeo
1: Theory of relativity explained in 7 mins
How does your production compare with the LondonCityGirl video? The audio has a few errors in the physics. What were
the errors? The discussion on mass is incorrect. Why? How would
you change the video to give a better model of mass, momentum and energy? Watch Video 2: Special Relativity:
Crash Course Physics #42 Watch Video 3: Professor Dave
Explains Which video is best (1) or (2) or (3)? Justify your answer. |